互动科普

量子光学的实验证明，相距遥远的两个事件彼此间相互影响的速度可以超过在它们之间传递的任何信号的速度。

对于研究量子力学的实验人员来说，怪事常常会变成现实。最近的一个例子来自对一种被称为非定域性(即“超距作用)的现象的研究。非定域性的观念对现代物理学的最根本的原理之一——没有任何东西的速度能够超过光速一一提出了质疑。

当位于一堵壁上的粒子消失，却又在几乎一瞬间在壁的另一侧重新出现时，上述原理便明显地遭到了破坏。在这里提一下Lewis Carroll是有益的。当Alice穿过镜子时，她的运动在某种意义上构成了一种超距作用(即非定域性)：她毫不费力地穿过一个固态物体的运动是瞬时性的。上述粒子的行为也具有同样奇怪的特点。如果我们试图求出该粒子的平均速度，便会发现它超过了光速。

这可能吗?现代物理学最著名的定律之一会这样轻易地遭到破坏吗?或者是不是我们的量子力学概念的形成或行进速度的概念出了毛病呢?为了回答这些同题，本文作者和其他一些研究人员最近进行了许多光学实验，以考察量子非定域性的某些表现形式。我们的注意力特别集中在非定域效应的三种表现形式上。在第一个实例中，我们让两个光子“赛跑”，其中一个光子必须穿过一道“壁”。在第二个例子中，我们考察如何给这种赛跑定时，从而证明每个光子同时沿着两条不同的赛跑路径行进。最后一个实验则揭示孪生光子的这一同时性行为是如何相互耦合的，即使当这对光子相距甚远以致任何信号都没有时间在它们之间传递时也是如此。

定域性和非定域性之间的区别与轨迹这一概念有关。例如，在经典世界中，一个滚动的槌球在每一时刻均有一个确定的位置。如果在每一时刻都拍摄一幅快照，然后将所有照片连在一起，则它们就形成了从运动员的槌到弓形小铁门的一条平滑而不间断的曲线，即运动轨迹。在这条轨迹的每一点上，槌球都有确定的速度，此速度与它的动能有关。如果槌球在平的场地上滚动，它就一直滚向它的目标。但如果槌球开始滚上坡，它的动能就转化为势能，其结果是滚动的速度越来越慢，最终停下来并回头向下滚。用物理学的术语来说，这样一种山坡称为势垒，因为槌球没有足够的能量翻过它，而且(从经典物理学的角度看)槌球总要往回滚。类似地，如果Alice没有用足够的力量去击槌球(或者去击卷缩着的刺猬，因为Carroll有刺猬)以使它们能撞穿一堵砖墙，则槌球就只能回弹过来。

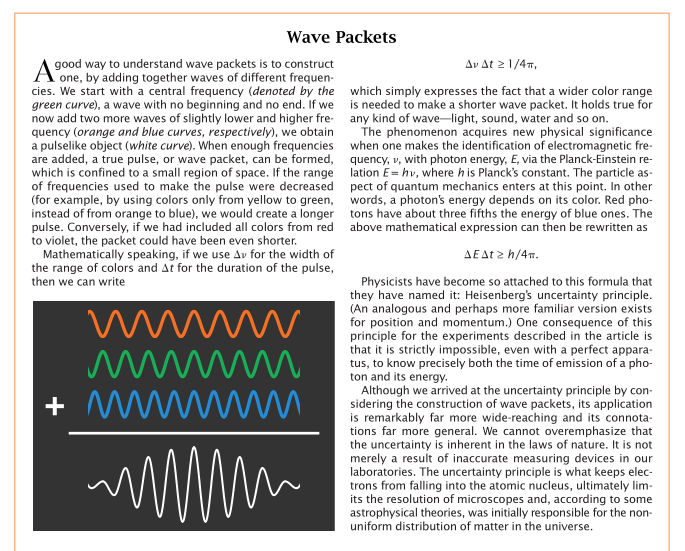
量子力学认为这一关于轨迹的概念是有同题的。与槌球的位置不同，量子力学粒子的位置不能描述为精确的数学点。相反，量子力学粒子最好用模糊的波包来表示。这种波包可看作类似于乌龟壳，因为它的形状是从其前沿向上升起，到达某一高度后又开始下降到其后沿。波包在沿着这一跨度的任一给定位置上的高度代表了粒子占据该位置的概率：波包的某一给定部分越高，则粒子落在该部分的可能性就越大。波包从前到后的宽度代表了粒子位置固有的不确定性(见图5)。然而，当粒子一旦在某一点上被检测到时，整个波包便消失了。量子力学不会告诉我们在此之前粒子位于何处。

位置上的这种不确定性导致了量子力学的最引人注目的推论之一。如果刺猬具有量子力学性质，那么位置的不确定性便使得这种动物有很小的(但却是完全实在的)可能性出现在墙的另一侧。这一过程被称作隧道效应，它在科学技术中起着重大作用。隧道效应在核聚变、某些高速电子器件，现有的最高分辨率显微镜以及某些宇宙学理论中具有关键的重要性。

虽然我们把这种效应取名为“Tunneling(有开挖隧道的意思)，但势垒却始终是完好无损的。事实上，如果一个粒子位于势垒之内，则它的动能将为负值由于速度与动能的平方根成正比，因此在隧道效应的场合必须对一个负数取平方根。这样，我们不可能说势垒中的粒子具有实在的速度。这就是为什么当刺猬穿到墙的另一侧之后并观看它从大白兔那里借来的表时，它的脸上会出现一副困惑的表情(正象本世纪三十年代以来的大多数物理学家那样)。刺猬看到了什么时间呢?换言之，它用了多长时间隧穿过势垒?

多年来人们曾多次尝试解答隧穿时间的问题，但没有一次尝试的结果获得普遍承认。我们的研究小组最近利用光子而不是刺猬完成了一项实验，此实验具体地确定了隧穿时间。

光子是构成所有各种光的基本粒子；一盏普通的电灯泡在十亿分之一秒的时间内可发射出一千亿以上的光子。我们的实验远不需要这样多的光子。为了进行测量，我们采用了一种同时发射一对光子的光源。

每个光子向着一台不同的检测器行进。在其中一个光子的行进路径上设置了势垒，而另一个光子则让其不受阻碍地自由飞行。在大多数情况下，第一个光子从势垒上反射回来并消失了；仅有其孪生光子被检测到。但是，偶尔第一个光子也会隧穿过势垒，这样两个光子都到达其各自的检测器。在这种情况下，我们就能比较它们的到达时间，从而看出隧穿过程需要用多长的时间。

势垒的角色由一个普通的光学器件——镜子——来扮演。不过，这个镜子与通常的家用镜子不同。(家庭用的镜子依靠一层金属涂膜，且可以吸收多达15％的入射光。)这种实验室用的镜子由两种不同类型的透明玻璃薄层交替排列而构成，光穿过这两种玻璃时的速度稍有不同。这些薄层相当于周期性的“速度挡板”的作用。单个地看，它们只不过是使光的速度放慢，但如果把它们组合起来并以适当间隔排列，则它们就形成了一个光实际上不能通过的区域。一个一微米厚(相当于人的典型头发丝的直径的百分之一)的多层复膜能把入射光光子能量(或光的颜色，二者是等价的)的99%反射回去。复膜是专门为此目的而设计的。我们的实验研究的就是剩下的这1％的光子，它们隧穿过镜子。

在收集数据的几天时间中，1百多万个光子一个接着一个地隧穿过了势垒。我们比较了隧穿光子的到达时间和不受阻碍地以光速行进的光子的到达时间。(光的速度极快，常规电子器件的计时速度比执行这一计时工作所要求的速度慢了几十万倍；我们采用的计时方法将在下面介绍量子非定域性的第二个例子时加以说明。)

结果是令人惊奇的：平均说来，隧穿光子比那些在空气中行进的光子先到达检测器，说明平均隧穿速度约为光速的1．7倍。这一结果似乎同经典的因果性概念相矛盾，因为根据爱因斯坦的相对论，没有任何信号的传播速度可以超过光速。如果信号跑得比光还快，那么从某些参考者的角度看来，结果就可能出现于原因之前。比如说，一盏灯可能在开关合上之前就亮了起来。

这种状况可以叙述得更精确一些。如果在某一确定时间你作出了打开一个启动门从而开始向一面镜子发射光子的决定，并且有另一个人坐在镜子的另一侧搜寻光子，那么要经过多长时间这另一个人才知道你已经打开了启动门?初看起来似乎是，既然光子隧穿的速度超过了光速，则她将在以理论上的最高速度行进的信号能够到达她之前就看见光，这样就违背了爱因斯坦的因果性观点。这一事态似乎暗示着一大类不寻常的、甚至十分古怪的通信技术。事实上，在比光还快影响下产生的推断曾促使二十世纪初期的某些物理学家提出对量子力学标准解释的一些替代方案。

有没有一种量子力学方法来摆脱这种两难困境呢?答案是肯定的，但它却使玩弄困果关系的这种令人兴奋的可能性不复存在。到现在为止，我们一直是在经典力学的框架内谈论光子的隧穿速度，就好象该速度是一个可直接观测的量。然而，海森堡的不确定性原理却指出情况并非如此。光子的发射时间不是精确限定的，它的确切位置及速度也是如此。事实上，光子的位置用一个钟形概率分布(即乌龟壳形曲线)来描述更恰当一些，该分布的宽度对应于其位置的不确定程度。

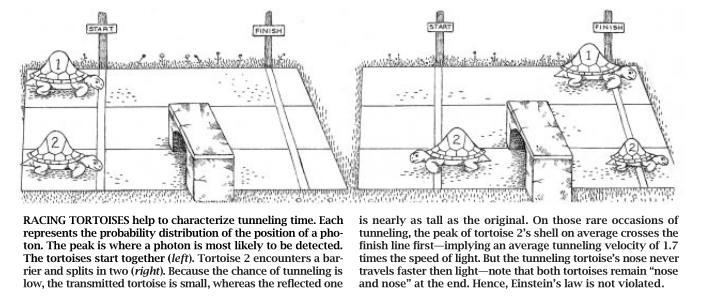
再用一个譬喻或许有助于说明问题。每个乌龟的鼻子在启动门打开的一刹那闻离开启动门。龟鼻的冒出标志着有可能观测到一个光子的最早时刻。在鼻子到达之前不可能收到任何信号。但是由于光子位置的不确定性，平均说来该光子经过一段短暂的延迟后才通过启动门。乌龟的主体部分(在此部分该光子更有可能被检测到)位于其鼻子之后。

为简单起见，我们将不受阻碍地到达检测器的光子的概率分布称为1号乌龟，而将隧穿光子的概率分布称为2号乌龟。当2号乌龟到达势垒时，它就分为两只较小的乌龟，即反射回起点的小乌龟和穿过势垒的小乌龟。这两只单个小乌龟合起来代表了单个光子的概率分布。当这个光于在某一位置上被检测到时，它的另一只小乌龟就立即消失了。反射回来的乌龟比隧穿乌龟大，因为光子反射回来的几率比透射过去的几率大(前面我们提到镜子有99％的机会将一个光射回去)。

我们观察到，2号乌龟龟壳的顶部(它代表了隧穿光于的最可能位置)比1号乌龟龟壳的顶部先到达终点但是2号乌龟的鼻子到达终点的时间一点也不比1号乌龟早。由于乌龟的鼻子以光速行进，因此标志启动门打开的光子的到达时间不可能早于因果关系所允许的时间(见图3)。

但是，在典型的实验中，龟的鼻子代表的是低概率区域，光子在此区域中被观察到的可能是极小的。光子的行踪(仅检测到一次)最好是1用龟壳顶部的位置来预测。因此，即：使两只乌龟的鼻子同时到达终点。2号乌龟龟壳的顶部仍领先于1号乌龟龟壳的顶部。(记住，透射过的乌龟比1号乌龟小。)因此，隧穿过势垒的光子比不受阻碍地以光速行进的光子先到达终点的可能性是极大的。我们的实验证实了这一预测。

但是我们不相信波包的任一部分会比光运动得快。相反，波包是在行进过程中被“整形”。直至出射的波峰主要由原先波包中位于前面的那一部分组成。隧穿光子的波包在任何一点上都不比自由行进的光子运动得更快。1982年，斯坦福大学的Steven Chu和当时在美国电报电话公司贝尔实验室的Stephen Wong观察到一种类似的整形效应。他们用含有许多光子的激光脉冲进行实验，发现成功穿越一个障碍的少数光子比那些能够自由运动的光子到达得早。人们可能会推测仅有每个脉冲的头几个光子被“允许”通过，这样就可以忽略整形效应。但是这一解释在我们的实验情况下是不可能的。因为我们一次仅研究一个光子。在检测到该光子的瞬间，这一整个光子立即跃变成波包的透射部分，它在一半以上的场合中先于其孪生部分到达终点。

虽然整形似乎解释了我们的观测结果。但是整形为什么会首先发生仍然是个问题。迄今还没有任何人对快速隧穿提出过任何物理解释。事实上，这个问题早在本世纪三十年代就曾困扰过研究人员，当时一些物理学家(如普林斯顿大学的Eugene Wigner)注意到量子理论似乎意味着存在这样高的隧穿速度。有些人认为这一预测所使用的近似必定不正确，而另一些人刚认为理论本身是正确的，但需要谨慎地进行解释。有些研究人员(特别是IBM公司TmasJ．Watch研究中心的MrkUSButtiker和RolfLandauer)提出，除开波包波峰的到达时间之外的另一些量(例如自旋粒子在隧穿时旋转过的角度)可能更适合于描述粒子在势垒内部 “用去”的时间。虽然量子力学可以预测一个粒子的平均到达时间，但它缺乏经典的轨迹概念，而没有这种概念的话，在某一区域中花去的时间这种说法的意义是不明确的。

隧穿现象的一个奇特性质为解释快速隧穿时间提供了暗示。按照理论，势垒宽度的增加不会使波包隧穿过势垒所需的时间变长。这一看法可以根据不确定性原理加以粗略地理解。具体地说，用于研究一个光子的时间越短，该光子能量的不确定程度便越大。即使向着一个势垒发射的光子不具备足够的能量穿越势垒，在某种意义上来说开始时也存在一个短暂的时间，在这段时间中粒子的能量是不确定的。这段时间内，该光子似乎能够暂时地借来足够的额外能量以使它越过势垒。这段宽限期的长短仅取决于借来的能量，而与势垒的宽度无关。无论势垒多宽，穿过势垒的渡越时间均不变。对于足够宽的势垒，表观穿越速度将超过光速。

很明显，为了使我们的测量工作有意义，我们的乌龟必须爬过完全相等的距离。实际上我们不得不把跑道拉直，使任何一只乌龟都无法利用内侧跑道的优势。这样，当我们在一个跑道上放置势垒时，任何减慢或加速都必定只由量子隧道效应所引起。设置两条相同跑道的一个办法是对于每条跑道测定光子从光源到检测器所需的时间。一旦这两个时间相等，我们就知道这两条路径的长度也相等。

但是用通常的跑表进行这种测量需要一个人的手每分钟动作将近一百亿亿(10的18次方)次。幸运的是，罗彻斯特大学的LeonardMandel及其同事们已经研究出了一种可以为我们的光子计时的干涉技术。

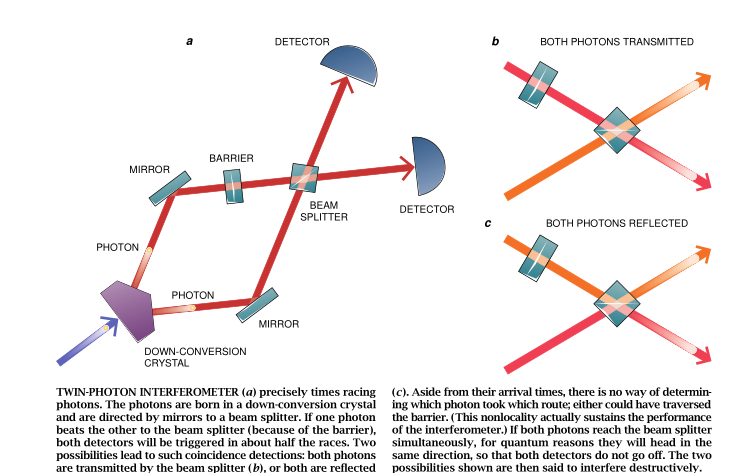
Mandel的量子跑表依靠一个称为分束器的光学器件(见图4)。这样一种器件将撞到它上面的光子中的一半反射，而让另一半透射过去。跑道的设置使得两个光子波包同时从启动门释放出来，并从相对的两侧向分束器行进，对于每一对光子，存在着四种可能性：两个光子都穿过分束器；两个光子都从分束器上反射；两个光子一起向一侧行进；或两个光子一起向另一侧行进。头两种可能性——两个光子都透射过分束器或都被分束器所反射一一导致所谓符合检测。每个光子各到达一台检测器(置于分束器的两侧)，两台检测器同时触发的时间相差精度为l0亿分之一秒。遗憾的是，这一时间分辨率涉及的是光子跑完整条跑道所用的时间，因而太粗糙了，没有什么用处。

那么分束器和检测器怎样帮助设定跑道呢?我们仅对一条跑道的长度进行调节，直至所有的符台检测都消失为止。这样我们便使光子同时到达分束器．实际上也就使两条跑道的长度相等了。很明显这种说法听起来有点古怪——毕竟，相等的跑道长度似乎意味着光子同时到达两个检测器。为什么这类事件出现反而是我们所期望的信号呢?

原因在于量子力学粒子彼此相互作用的方式。自然界的所有粒子不是玻色子就是费米子。全同费米子(例如电子)服从泡利不相容原理；根据此原理．这类粒子中的任何两个在同一时刻不能占据相同的位置。相反，玻色(例如光子)便喜欢聚在一起。因此，两个光子在同时到达分束器之后，便倾向于朝相同的方向行进。这一倾向性使检测到的符合发生的次数比两个光子独行动时或在不同时间到达分束器时的符合发生的次数少(在理想的实验中将减少到一次也没有)。

因此，为确保光子进行公平的竞赛，我们对两条路径长度中的一条进行调节。在这一个过程中，符合检测的发生率下降，其最小值出现在两个光子到达分束器所用的时间完全相同的时候。下降的宽度(它是限制我们实验的分辨率的因素)相当于光子波包的大小——通常为光在10的14次方分之几秒内行进的距离。

只有在我们确知两条路径的长度相等以后，我们才设置势垒并开始赛跑。此时我们发现，符合率不再停留在最小值，这意味着两个光子中有个先到达分束器。要想恢复最小值，我们必须延长隧穿光子的路径。这一修正表明光子穿越势垒所用的时间比在空气中行进所用的时间少。

尽管研究人员为这场赛跑设计了光子的跑道和巧妙的计时工具，这场赛跑本来仍然是很难进行的。它之能够得以进行这一事实构成了对非定域性原理的又一证实。如果没有非定域性，就不可能对这场赛跑进行精确的计时。为了最精确地测定一个光子发射时间。很明显人们希望光子波包尽可能短；但是，不确定性原理宣称，对光子的发射时间测定得越准确，则其能量(即颜色)的不确定程度就越大(见图5)。

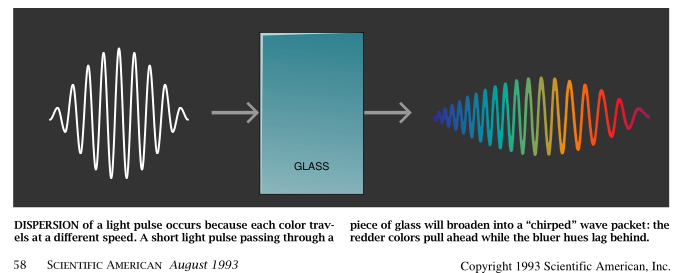
由于不确定性原理的缘故，我们的实验中必然出现一种不可避免的折衷。构成一个光子的颜色在任何一种玻璃中都将发生色散，使波包变宽。从而降低计时的精度。发生色散的原因是不同颜色的光在玻璃中以不同的速度传播——蓝光通常比红光要慢。色散的一个众所周知的例子是自光被棱镜分解成其各种组份颜色。

当一个短的光脉冲穿过某种色散介质时(如势垒或用来控制光的行进方向的一个玻璃元件)。它就展宽成一个“啁啾”脉冲，即其较红的分量向前移动，而较蓝的分量则落在后面(见图6)。简单的计算表明，我们的光子脉冲在穿过一英寸厚的玻璃时其宽度将增加3倍。这种展宽效应的存在本来会使我们几乎不可能判定哪只乌龟首先越过终点线。出乎意外的是，光子脉冲的展宽实际上并未降低我们的计时的精确度。

奥妙在于我们提出的量子非定域性的第二个实例。事实上两个孪生光子必定都同时在两条路径上行进。其结果是使各种潜在的计时误差互相抵消了，这真是几乎有点令人感到不可思议。

为了理解这种抵消效应，我们需要考察一下我们的光子对的一种特殊性质。这些光子对诞生于物理学家们所谓的“自发参量下变频”的过程。当光子进入一种非线性光学性质的晶体时，便会出现这一过程。这类晶体可以吸收一个光子而发射另外的一对光子来代替它，每个新光子的能量大约为母体光子的一半(这就是“下变频”这一术语的意义)例如，一个紫外光子将产生两个红外光子。这两个光子同时发射。且其能量之和恰好等于母体光子的能量。换言之，光子对的颜色是相关的——如果一个光子稍微蓝一些(因而在玻璃中行进得更慢一些)，那么另一个光子就必定稍微红一些(因而在玻璃中必定行进得快一些)。

人们可能会以为子代光子的差别将影响赛跑的结局——一只乌龟可能比另一只跑得更快一些。但是由于非定域性，两个光子之间的任何差别均被证明是不相干的。关键在于，任何一台检测器都没有办法确定哪个光子走的哪条路径。两个光子中的任一个都可能越过势垒。

有两个或更多个共存的可能性——这些可能性导致同样的最终结局一一产生了所谓的“干涉效应”。在干涉效应中，每个光子都同时走两条路径，而且这两种可能性互相干涉。也就是说，穿过玻璃的光子为较红(也就是较快)光子的可能性与它为较蓝(也就是较慢)光子的可能性互相干涉。其结果是速度差别和色散效应都抵消了，单个光子脉冲的色散展宽就不再成为一个影响因素。如果自然界的行为是定域性的，那么我们要进行任何测量就会非常困难。只有一个办法可以描述所发生的情况，那就是说每个孪生光子均经过设有势垒和未设势垒的两条路径，而这种情况正是非定域性的例证。

到现在为止我们已讨论了我们的量子实验得出的两个非定域性的结果。第一个是测量隧穿时间，它要求两个光子在完全相间的时刻开始赛跑。第二个是色散抵消效应．它依靠赛跑光子的能量的精确相关性。换言之，我们可以说光子在能量(即它们做什么)和时间(即它们什么时候做)上是相关的。我们关于非定域性的最后一个例子实际上是前面两个例子的结合。具体地说就是，不论两个光子相距多远，一个光于都对其孪生光子的行为立即“作出反应”。

见多识广的读者到此可能会提出异议，宣称海森堡的不确定性原理表明同时精确测定时间和能量是不可能的。对于单个粒子而言，他们的看法是正确的。但是，对于两个粒子，量子力学允许我们同时确定其发射时间的差和其能量的和。即使这两个粒子的时问与能量都不确定。这一事实促使爱因斯坦、BorisPodolsky和NathanRosen得出结论说量子力学是不完备的理论。1935年，他们提出了个假想实验，以证明量子力学具有他们所认为的缺陷。

这几位持不同意见的物理学家指出，如果相信量子力学的话．那么由下变频之类的过程产生的任何两个粒子都应是耦合的。例如，假定我们测量了一个粒子的发射时间由于两个粒子间存在紧密的时间相关性，我们可以有把握地预言另一个粒的发射时间而无需扰动它。我们也可以直接测量第二个粒子的能量，随后推断出第一个粒子的能量。这样通过某种方式我们得以精确地同时测定每个粒子的能量和时间——实际违背了不确定性原理，我们如何能够认识这类相关性并解决这悖论呢?

基本上说来存在两种解决方案。第一种方案认为存在着爱因斯坦所谓的“占怪的超距作用”按照这一方案，全部情况都可以用量子力学对粒子的描述来解释。比如说在进行了一次能量测量之前，没有任何特定的时间或能量同任何光子相关联。在进行了一次能量测量后，仅有一个能量被观测到。由于这两个光子的能量之和等于母体光子的确定的能量，所以先前未被确定的一个孪生光子的能量——我们并未测量这一能量——必然立即跃变为能量守恒定律所要求的值。不论第二个光子已行进了多远，这一非定域的“坍缩”都会发生，不确定性原理没有受到破坏，因为我们仅能确定两个变量中的一个：对能量的测量扰乱了系统，立即使时间出现了新的不确定性。

当然，如果还有另一种更简单的办法可以理解相关性的话，那么上面这样一个古怪的非定域性模型就不会被人们所接受了。一种更为直观的解释是，两个孪生光子在确定的相关时间离开发射源，携带着确定的相关能量。量子力学不能同时确定这些性质的事实仅仅表明这一理论是不完备的。

爱因斯坦、Podolsky和Rosen赞同后一种解释。对他们来说，粒子对之间被观测到的相关性中根本不存在任何非定域性的因素，因为每个粒子的性质都是在发射之时就决定了的。量子力学仅作为一种概率理论(即一种光子社会学)是正确的，它不可能完全描述所有的单个粒子。可以想象存在着一种能预测所有可能测量的具体结果并证明粒子行为具有定域性的基本理论。这样一种理论将以某个尚待发现的隐变量为基础。1964年，在日内瓦附近的欧洲粒子物理实验室的John S．Bell证明了一条定理，该定理表明，对定域的隐变量的任何引用所得出的预测都和量子力学给出的预测不同。

从那时以来，实验结果都支持非定域的(量子力学的)描述而与爱因斯坦、Podolsky和Rosen的直观描述相矛盾。这方面的开创性工作的主要功劳归于伯克利加利福尼亚太学的John Clauser以及目前在法国奥赛光学研究所的Alain Aspect领导的研究小组。在七十年代和八十年代初，他们考察了光子的偏振相关性。英国皇家信号与雷达研究所的JohnG．Rarity和PaulR．Tapster的更近一些时候的研究工作考察了孪生光子的动量之间的相关性。我们的研究小组则把这些检验又向前推进了一步。根据约翰斯·霍普金斯大学的James D．Franson 1989年提出的一个设想，我们进行了一项实验以确定是否某个定域的隐变量模型(而非量子力学)能够解释能量和时间的相关性。

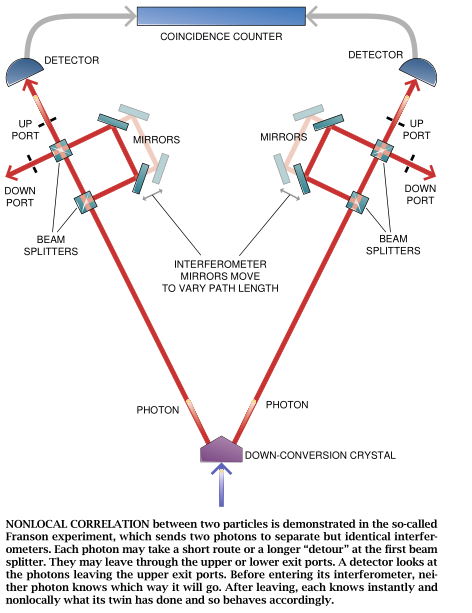
在我们的实验中，从下变频晶体出来的孪生光子对被分别发送到相同的干涉仪上(见图7)。每台干涉仪设计得颇象带一段任选弯道的州际公路。光子可以走较短的路径，从其发射源直接到达目的地。但它也可走较长的弯道(其长度是可调的)，也就是绕道经过其它站后再继续赶路。

现在看看当我们把一对光子的成员发送到这些干涉仪时会出现什么情况。每个光子将随机地选择走较长的路(即经过弯道)或较短的直路。在走过这两条路径中的某一条后，光子可能通过两个孔(一个标以“上”，而另一个标以“下”)中的某一个离开干涉仪。我们观测到，每个光子通过上孔离开干涉仪的可能性与通过下孔离开干涉仪的可能性一样大。因此我们可以直观地假定，光子选择某一出口与其孪生光子在另一台干涉仪中所作的出口选择无关。其实错了，事实上我们观察到每个光子在其离开干涉仪时所走的路径之间存在着强烈的相关性。例如，当弯道长度为某些值时，只要左边的光子通过上出口孔离开，则右边的光子也通过自己这边的上出口孔离开。

人们或许会猜测这一相关性从一开始就是存在的，就好象在一只手里捏着一个白兵而在另一只手里捏着一个黑兵一样。由于它们的颜色从一开始就完全确定了，因此，当我们一发现某只手里拿的是白兵时，立即就满有把握地知道另一只手里拿的必定是黑兵，这是一点也不令人奇怪的。

但是一种固有的相关性却不能解释我们实验中所发生的奇怪得多的真实情况；改变任一台干涉仪中的路径长度，我们就可以调节相关性的性质。我们可以从两个光子总是通过各自的干涉仪的相应的出口孔(即同时通过上出口孔或同时通过下出口孔)这种情况平稳地达到两个光始终通过相反的出孔这一情况。原则上说，即使我们在光子已经离开发射源后才调节光路长度，这样一种相关性也是存在的。换言之，在进入干涉仪之前，没有一个光子知道它将必须走哪条路径——但是在离开干涉仪时，每个光子立即地(非定域地)知道其孪生光子所走的路径并相应地采取自己的行动。

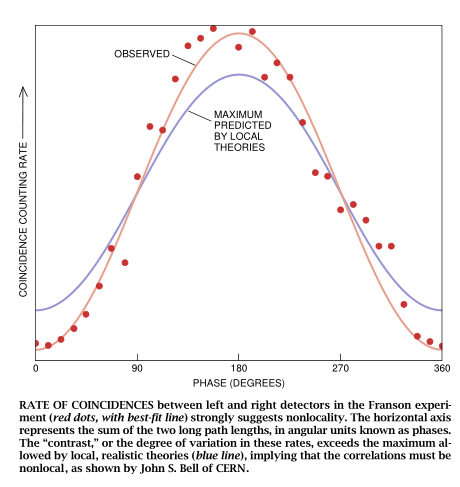
为了分析这相关性，我们考察了光子在相同的时间离开各自的干涉仪后，并在置于两台干涉仪的上出口孔处的检测器之间产生符合计数的频度。改变任一条长臂光路的长度并不会使每一台检测器上的检出率发生变化，但它却对符合计数率发生影响，从而表明了每个光子对的相关行为。这一改变产生了类似于传统的双缝干涉仪所产生的明暗线条(这些线条证实了粒子的波动性)的干涉条纹。

在我们的实验中，这些条纹暗示了一种奇特的干涉效应。前面曾提到，干涉可以表示为两个或多个导致相同最终结果的无法区分的共存可能性互相作用的结果。(回忆一下我们关于非定域性的第二个例子，其中每个光子同时沿两条不同的路径行进，从而产生干涉)在目前这种情况下，存在发生符合计数的两条可能途径：或者是两个光子都走过较短的路径，或者是两个光子都走过较长的路径(在一个光子沿较短路径行进而另一个光子沿较长路径行进的情况下，这两个光子在不同时刻到达检测器，因而不会相互干涉，我们采用电子手段除去这类计数)

这两种可能性的共存暗示了一个在经典物理学看来是荒谬的情景。由于每个光子在沿着长短两条路径都走过后同时到达检测器，因此每个光子发射了“两次”——一次是对于较短的路径而另一次是对于较长的路径。

为了看出这一点，我们作一个类比，并假定你在其中扮演一个探测器的角色。你收到在另一个大陆上的朋友寄来的一封信。你知道这封信是通过航空或海路送来的，这表明该信于一周前发出(由航空送来)，或者于一个月前发出(由海路送来)。为了使干涉效应存在，这一封信必须在两个时刻都发出，自然，从经典角度看，这种可能性是荒唐的。但是在我们的实验中，观察到干涉条纹这一事实表明孪生光子中的每一个都有两个无法区别的从晶体中的发射时间。每个光子有两个生日。

更重要的是，干涉条纹的精确形状可用来区分量子力学和任何可以想象出来的定域隐变量理论(在这种理论中，每个光子可能比如说一诞生就有着确定的能量或已经知道要走哪个出口孔。)根据Bell推导出来的限制，任何一种隐变量理论都不可能预测其“对比度”大于71％的正弦形条纹——也就是说，亮条纹与暗条纹之间的强度差有着具体的限度。但是，我们的数据却显示了对比度约为90%的条纹。如果再作一些合理的补充假定，就可以从这些数据得出结论：爱因斯坦及其追随者提出的直观、定域和现实的图景是错误的；如果不承认某一方的一次测量的结果非定域地取决于另一方的一次测量的结果，就不可能解释观察到的实验结果。

那么爱因斯坦的相对论是否岌岌可危了呢?奇怪的是并非如此，原因在于没有任何办法可能利用粒子间的相关性来发送比光速快的信号。其理由是，每个光子究竟是到达其检测器还是经过下出口孔离开是一个随机的结果。只有在比较了两台检测器的显然是随机的计数记录后(这就必定要把我们的数据汇集在一起)，我们才能注意到非定域的相关性。因果性原理依然未受到破坏。

科幻小说的爱好者们在得知比光还快的通信看来仍是不可能实现的之后或许会感到沮丧。然而有些科学家已试图充分利用这种情况。他们提出将相关性的随机性用于各种密码方案中。用这样的量子密码术系统产生的代码将是绝对无法破译的。(见《科学》1993年2月号的量子密码术”一文)

到现在为止我们已经在3个不同的例子中观察到非定域性。第一，在隧穿过程中，光子能够通过某种方式感知到势垒的另一侧，并且不论势垒有多厚，它都能在相同的时间里穿越势垒。第二，在高分辨率的定时实验中，色散的抵消依赖于两个光子中的每一个都走过干涉仪中的两条路径。而在我们讨论的最后一个实验中，两个光子离开干涉仪后的耦合行为证明了这两个光子存在着能量和时间的非定域的相关性。虽然在我们的实验中两个光子仅相隔几英尺，但量子力学却预言无论两台干涉仪相距多远，这种相关性都会被观测到。

大自然不知怎么的总是巧妙地避免任何与因果性概念相矛盾的事情发生，因为决不可能利用上述效应中的任何一种来发送比光速还快的信号。定域性的相对论和非定域性的量子力学的脆弱共存已经安然度过了又一次风暴。