互动科普

现今人们最熟悉的锥面，大概要算是用来盛冰淇淋的那种能吃下去的锥形蛋卷了。但历史上锥面的辉煌却完全在另外一些更高级的层次上。古希腊人已经熟悉锥面的几何性质，这主要是因为用一个平面去截锥面可以构造出漂亮的圆锥曲线。古希腊人很喜欢这些圆锥曲线——包括椭圆、抛物线和双曲线——的精巧的几何性质，并发现了如何利用它们去解决一些单靠圆规直尺无法解决的问题。

这些问题包括三等分角问题(即将给定的一个角分为相等的三个角)和倍立方体问题(即作一个立方体，使其体积为已知立方体体积的两倍。)这两个问题均可简化为解一个三次方程(三次方程就是其未知数的最高次数为3的方程)。圆锥曲线之所以能够解决这些问题，是因为两条圆锥曲线的交点对应于三次方程和四次方程的解。而圆规和直尺则只能解二次方程。

数学家们对锥面本身的兴趣通常不及对这些平面截线的兴趣大，这可能是因为锥面本身的形状太简单了。对于这种不起眼的立体，是否还有什么新东西可说呢？事实上肯定是有的。1999年5月，住在英国波尔多镇的一位本专栏读者C．J．Roberts写信给我，介绍了一种他称为“球锥”(Sphericon)的非常新奇的立体。他甚至把两个球锥附在信中寄来。

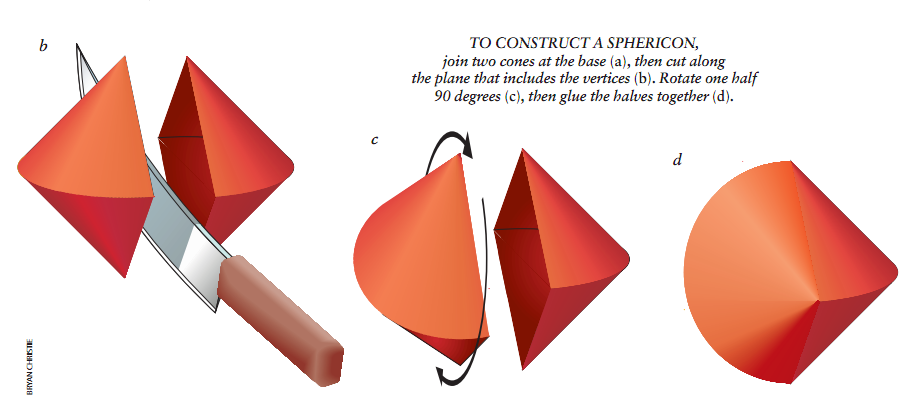
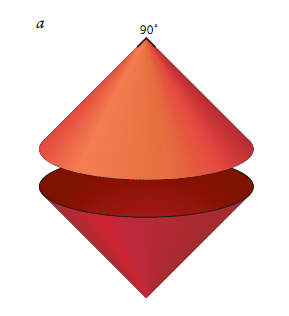
图1所示的球锥是一个双锥(即把两个相同的锥面底对底合在一起所得的立体)，但搞了一点花样。它的制作很简单。如果你把双锥沿着过两个顶点的平面切开，你就得到一个菱形截面，即四条边相等的平行四边形。如果你使用的锥面的形状恰好合适，你将得到一个正方形截面。与其它所有菱形不同，正方形还有另一种对称性把正方形转过一个直角后，它又回到其原先的形状上。因此你可以沿着中间切开这样一个双锥，把所得的两半立体中的一半转过90度，然后再把这两半重新粘在一起。这样就得到球锥了。由于搞了这一花样，现在它就不是双锥，而是一个令人们兴趣大增的怪物。以前我从未见到有任何文献曾提到过这种形状的立体，但是，如果我对于它的新颖性的说法有错的话，相信某位见多识广的读者会很快提醒我。

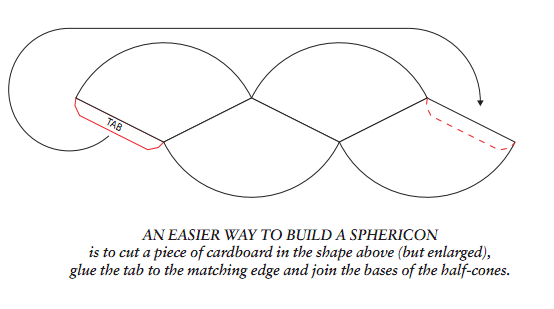
球锥可以用一块薄纸板来做。把这块纸板剪成由4个相同的扇形构成的一，种形状，4个扇形连接在一起呈交错排列(见图2)。设计这种图形时需要进行的主要计算是求出扇形的两条直边之间的夹角。假定每条边的长度为1。如果双锥的截面为正方形，则根据毕达哥拉斯定理，每个分锥的底面直径为√2。因此底面周长为π√2扇形弧的长度为该底面周长的一半(因为你在做球锥时是把把双锥切成两半)。这样可以求出扇形的角为π√2弧度，即90度，约等于127.28度。

如果你剪出图2中所示的图形，你就可以把扇形卷成、锥，并把图中所示的小舌片粘到对应的边缘上。只需稍微调整一下，半锥面的底就能天衣无缝地配合在一起，然你可以用胶粘带把接缝粘好。

球锥的第一个乐趣就是，它能滚动！把一个锥体放在平坦表面上时它就成圆圈地滚动。双锥可以沿顺时针方向或反时针方向的圆形路线滚动，但是只有在你把它迅速地像保龄球那样滚出时或把它放在轨道上时它才会沿直线行进。球锥则可以表演受控摆动，其摆动路线平均说来是沿直线行进。首先是一个锥面扇形与平坦表面接触，然后是另一个锥面扇形与平坦表面接触。因此，当球锥向前运动时，它轮流朝左右摆动。让球锥从一个缓慢倾斜的斜面顶部出发，观看它如何摇摇摆摆地滚下去是特别有趣的。在读了Roberts那封来信后，我花了半个小时的时间同其它几位数学家一起兴高采烈地在一个桌子上把球锥滚来滚去。

这封来信还提到了球锥的几种令人着迷的特性：它有一个连续的表面，而且一个球锥可以绕着另一个球锥无休止地滚下去。我对此极感兴趣，写信请Roberts提供更多资料，而他则在回信时寄来一个庞大而轻飘飘的纸板箱。纸板箱里装着由50个球锥组成的巨大点阵结构，这些球锥用透明胶十分整齐地装配起来。这种点阵结构同晶体的原子点阵一样，在三维方向上无限地重复下去。

球锥之所以具有如此漂亮的几何特性，原因之一在于它的四条“棱”——即其组份扇形相交的线——正好落在一个正八面体的四条棱上。这个正八面体的另外四条棱则对应于扇形顶角的平分线。而正八面体又与立方体密切相关：如果你在一个立方体每一面的中心画上一点，然后用直线把这些点联起来。你就得到一个正八面体。当然，立方体可以用一种规则的方向堆积起来，形成平坦的一层或充满三维空间。

今年47岁的Roberts在大约30年前发明了球锥。当他在学校读书时几何就是他的强项，而他参加工作后最初就是当一名木工学徒。因此，毫不奇怪，他的第一个球锥是用木头刻出来的。他的出发点是大名鼎鼎的Mobius带，也就是把一根纸带扭转180度后再把两端粘接起来所得的图形。Roberts意识到，由于纸有一定的厚度，因此纸带的横截面实际上是一个长而薄的矩形。如果你把横截面变成一个正方形，那么就可以在只转90度——而不是180度——之后把两端接起来，得到一个其外表面为单一的弯曲表面的立体。然而，这一立体的中央有一个洞：它是一个环。是否存在一种不是环而有一个单一的弯曲表面的立体呢？一天，当Roberts在对一段横截面为正方形的木料进行加工时，他开始考虑绕着木料的端头刨出一条曲线以使木料的一面与下一个面接合起来。在木料的两端进行这样的加工，再去掉中间的木料，就得到一个球锥。

Roberts用红木做了一个球锥，并把它送给了他的姐姐，后者一直珍藏着这个球锥。后来他就忘掉了这个课题。1997年，我作了一系列电视数学演讲，谈到了对称性的问题。此时Roberts对球锥的兴趣又被重新点燃，并给我写了信。

如果让两个球锥彼此挨在一起，它们就可以贴着彼此的表面滚动。把四个球锥布置在一个正方形的区域中，它们就可以同时互相绕着滚动。8个球锥可以布置在一个球锥的表面上，这样外侧的任何一个球锥都可以在中央那个球锥的表面上滚动。

球锥的各种可能布置方式看来是无穷无尽的。现在我打算让读者们自己去体验一下摆弄这种极其巧妙的数学玩具并发明种种新模式的乐趣。