互动科普

当我还是物理系的学生时，我的大部分时间都用在研究子虚乌有的东西上，诸如无摩擦力的滑轮、无质量的弹簧以及不随高度而变的重力等。科学家们早就意识到，真实的系统与其环境之间存在着一些难于进行实际测量的相互作用，而随着时间的推移这些效应就逐渐积累起来。因此我们知道，理想的解法仅能在一定的时间内描述系统。而我们所不知道的则是这一段时间可能有多短。

在八十年代，研究人员了解到，对于许多真实系统，自然界中不计其数的无法控制的复杂因素将使观测结果很快就同预测值产生分歧。例如，你可以尽可能多的测量温度、压力和风速读数，想测量多少就测量多少，但你就是无法掌握足够的信息来精确预测七天以后的天气。其理由在于，许多微小扰动——甚至比如说一架喷气飞机飞过盐湖城上空时引起的扰动——其效应都可能极其迅速地积累起来，速度之快远超过科学家们的预想，从而使天气发生无法预测的变化。迅速地进入无法预测状态的系统形象地称为“混沌“系统。

现在，由纽约州立大学锡拉丘兹保健科学研究中心神经科学与生理学教授Mahlon Kriebel开发了一项讨人喜欢的装置，你可以住自己家里的厨房桌子上探索混沌的种种复杂微妙的特性。Kriebel的装置是另一个的混沌实例一一滴水龙头的慢功作型式。Kriebel让有颜色的水滴一滴一滴地穿过矿物油降下，以减缓它们的速度，从而使我们很易观测到研究混沌的开端。

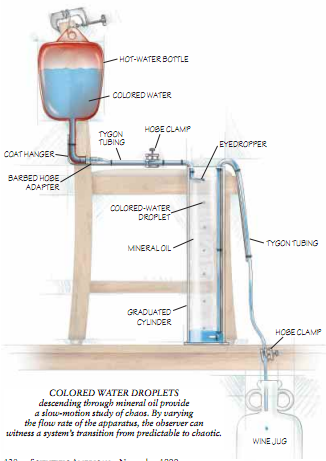
一个容积为l千立方厘米的量筒可以作盛矿物油的理想容器。不过可以用一个高的透明花瓶来盛矿物油。至于用来盛有色水的容器，可以用一个接自管道的热水瓶。把管道锯掉，用一个有倒刺的软管接头将其接在一段聚乙烯管上。你将需要一个软管夹来控制水经过管道和喷嘴的流速。你所需要的软管接头、软管火和管道几能住任何一家五金店买到。为了使热水瓶的何置比喷嘴高出一大截，我把热水瓶固定在一把椅子的靠背上，然后把椅子放在厨房桌子上。

Kriebel用一个吸量管的尖头做成了他的喷嘴，但是眼药滴管更容易弄到。眼药滴管的开口太大，因此我用蜡烛的蜡填满管的尖头，然后用一根加热了的缝衣针在蜡上熔化出一个微小的孔。用一把钳子将针夹住，使它的尖头抵住蜡上，并用一个热的烙铁往靠近滴眼管的地方碰到缝衣针上。稳稳地、不停地对针施加压，很快就能把针刺入蜡塞中。在喷嘴做成后，将其插入聚乙烯管中，并用足量的鱼缸用水泥使它们之间的连接牢固。

下一步，在把管道放好后需要将其固定住，为此，你可以把它拴在一段衣架上。注意要用缝衣线而不要用绞合线，因为后者散落出的纤维会弄脏矿物油。然后将其装入量筒中，使喷嘴的出口孔中心大约位于量筒顶端以下10厘米(4英寸)的地方。

把另一段聚乙烯管拴在另一个衣架上，并把它的一端放入量筒的底部。用软管夹把聚乙烯管的另一端夹住，并将其置于一个空的酒壶中。这一装置将使你能够通过虹吸作用把量筒底部收集的一部分有色水引到酒壶中，这样就可以反复把有色水送回热水瓶。

向量筒中注入矿物油(矿物油可从当地药店购得)，使矿物油刚好盖过喷嘴。然后用食物色素将水染上颜色，把这种带色的水注入热水瓶中。把上面那个软管夹稍微松开一点点，让水滴在喷嘴上慢慢形成，然后穿过矿物油掉下去现在你就已经作好准备，可以进入混沌遨游了。

当流速处于最低水平时，液滴全是同样的大小，这样它们掉下去的速率也基本是相同的。液滴一颗接一颗地落到量简底部，产生出一种可以记录为1，1，1，1，……的模式。

把流速稍微提高一点，液滴的大小就开始波动。较大的液滴在矿物油中下落的速度比较小的液滴快(前者的沉降末速度较高，是因为它们的单位表面积的质量较大)，因此它们将追上较小的液滴并进入较小的液滴中，这样我们将看到两个两个的液滴成一团地掉到量筒底部。在这样的流速下产生的模式为2，2，2，2，……。如果你把流速再提高一点，你可能会找到一个使液滴三个三个成一团地掉到量筒底部的流速。

在更高的流速下，这一过程就开始陷入混乱的局面，所记录的数据变得无法预测，但也不是随机的。为了弄清其原因，我们可以看看掷骰子的情况。骰子的滚动和水滴的掉下有一点是相似的，即它们都与一些极难掌握的因素有关。在骰子离开你的手时稍微改变一下它转动的速度或抛出的轨迹，它滚动的情况就可能完全不同了。类似地，水滴的大小和它下落的速率与一些无法控制的因素有关，例如当它同水流分离时它的振动情况以及喷嘴内压力的波动等。

然而，真正的随机过程是完全不可预测的。不论你在某一瞬间观测到些什么情况，它都同先前出现的情况毫无关系，也对以后发生的情况不产生任何影响。从这种意义上说，掷骰子是随机的。这是因为，掷出比如说1点的可能性永远是六分之一，不论这个骰子先前掷出的是几点。但是水滴掉下的情况就不同了，因为，尽管一个状态可能无法决定下一个状态，但它可以影响下一个状态。

例如，如果我连续不断地掷一个骰子，最终我将掷出两个连续的1点。但是在较高的流速下，我从未观察到两个单独的水滴一个接一个地落到量筒底部。因此我得出结论，搞出一个单独的水滴必将使系统进入一种只产生多个水滴的状态。换言之，如果一个单独的水滴掉到量筒底部，其后必然跟着若干水滴成团地掉下来。至少这就是某种信息。而对于此后发生的情况，我知道得就更少了。每一状态都影响下一状态，但其结果很快就变得越来越难以掌握，这就是混沌出现的标志。混沌介于无摩擦的摆完全可预测的特性与掷骰子的纯粹随机性这两者之间。

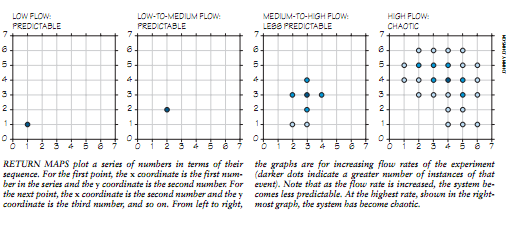
利用一种名为“返回图”(return map)的特殊图形，很容易发现混沌系统。对于水滴数据，把数据序列中的第一个数作为横座标，第二个数作为纵座标，绘出第一个点。画第二个点时，以数据序列中的第二个数作为横座标，第三个数作为纵座标。这样一直进行下去直到把所有数据都用完。在流速较低的龙头稳定地滴水时，所有的点都聚集在一个位置附近。对于随机的数据，所有各种数对出现的可能性是相同的，因此这些点将散布在整个返回图上。另一方面，混沌系统不是随机的，由于每一事件都影响紧随其后的一个事件，因此某些组合出现的可能性比其它组合出现的可能性大。如果这种联系相当紧密，返回图上的某些区域内将完全没有点。

返回图可以为我们打开一个充满了混沌乐趣的新世界。事实上，无数的日常现象都是混沌的，例如一条繁华街道上路人经过的时间间隔，一根藤上的花之间的距离以及猫身上的条纹之间的间距等。读者可以绘出这些变量的返回图，看看我们周围的世界究竟混沌到何种地步。