互动科普

数学家们认为他们研究的对象是美妙的，但许多人发现这种说法值得怀疑。可以用多种方法来描述小学的算术课或代数课，但大多数的数学的学生恐怕不会想到用“美妙”这个词来形容它们。不过，确实存在多种层次的数学美。一般人可能觉得他们很难欣赏一项令人满意的数学证明所蕴含的逻辑美。然而几何图形的美妙则与视觉艺术：一特别是雕塑的美学特性很接近，也更易为数学界以外的人所理解。

我以前在本专栏上曾探讨过受数学启发的雕塑作品的问题[参看本刊1996年9月号“数学游戏”专栏“A1an St．George的雕塑”一文]。那篇文章引来的众多读者来信表明，存在着种类多得令人吃惊的数学艺术。把整整一年的数学游戏专栏全都用来讨论这些问题也不会嫌多。在本期专栏中，我将考察最小曲面的数学性质与密苏里州戈瓦的艺术家Brent Collins制作的精美层板雕塑之间的关系。读者们将会看到，此故事也将提出关于真实艺术与虚拟艺术之间关系的若干关键问题。

八十年代，Collins在创作一些神奇的抽象雕塑时，完全没有有意要赋予这些雕塑以数学意义。然而，渐渐地他开始意识到，他一直在凭直觉倾向于使他的雕塑的各条棱之间的表面积达到最小。实际上他是在复现某些基本的拓扑图形。1995年Collins与伯克利加利福尼亚大学的计算机科学家Carlo H．Sequin携手合作，探讨了其艺术作品的数学联系。1997年《Leonardo》杂志详细介绍了他们的合作经过。

他们研究的关键图形是鞍面，即一种平滑的扭曲表面，其形状与你骑马时所坐的马鞍相似。鞍面是最小曲面的基本成份。对数学家来说，最小曲面是在满足某一约束条件的情况下具有最小表面积的曲面。(约束条件的作用是防止表面积缩小到零:例如，曲面必须张在某一给定曲线上。)

作为物理上的类比，我们可以把一段铁丝弯成曲线的形状将其浸入肥皂水中并观察所得的肥皂膜的形状。即使我们把这段铁丝弯成一些形状复杂的二维环圈和结，肥皂膜也始终是看起来十分漂亮而且显得很匀称。此外，肥皂膜处处呈鞍面的形状。这一性质是面积最小化造成的一一面积最小化迫使表面具有零曲率。零曲率并不意味着该表面是平的:它只是意味着每一点周围的表面具有鞍面的形状即沿一个方向朝上弯而沿另一个方向朝下弯。

Collins从鞍面形成的曲面着手，但很快就进而研究一些更复杂的图形，它们涉及数学家们所谓的“猴鞍面”。顾名思义，猴鞍面就是一种形状古怪的可供猴子骑在上面的鞍面——它在三个方向上是向下弯的，其中两个留出猴子放腿的地方，另一个则留出猴子放尾巴的地方

为了了解Co11ins如何把这些图形融入其作品中，我们来看看他在1995年完成的“双曲六边形”这一作品。双曲六边形由6个标准的鞍面构成，这岛鞍面互相连接起来形成环状。此雕塑与一种名为“Scherk塔” (Scherktower)的最小曲面有密切的关系。Scherk塔由一系列鞍面互相连接起来而构成，这且鞍面形成了若干开口方向交错排列的洞。

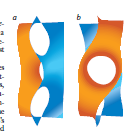
Collins和Sequin进行的讨论产生了一种令人注目的新结构——把Scherk塔扭转90度，后再把它的两端连接起来。这一操作有点像墨比乌斯带，也就是把一张纸条扭转180度后将它的两端连接起来。把纸条扭转就使得纸条的两面彼此合并起来，这样，当你从纸条的一面开始把纸条涂成红色时，只要你一直涂下去，最终就不得不把纸条的"另一面"也涂成红色。也就是说，墨比乌斯带是只有一个面的曲面。未扭转的Scherk塔类似于通常的纸条，它有两个不同的面，可各自涂成不同的颜色。双曲六边形也是如此。但是，用扭转后的Scherki塔构成的相应曲面则与墨比乌斯带相似，只有一个面。

Scherk塔的顶部和底部边缘各自形成十字交叉形，因此，如果Scherk扭转的角度为90度的整数倍，则它的顶端和底能完美地拼合起来。但是这一扭转还必须考虑到Scherk塔的洞的问题。由于Scherk塔的洞的开口方向是交错排列的，因此，奇数层的Scherk塔扭转的角度只能为90度的奇数倍而偶数层的scherk塔扭转的角度只能为90度的偶数倍。Collins1996年创作的雕塑“双曲二叶形”就是把一个3层的Scherk塔扭转270度后再把它的两端连接起来所得的超环面。

Sequin把这些图形命名为“Scherk-Collins曲面”。通过用数学语言表述Co11ins的概念，可以系统地设计出各种新的变种。数学上的处理也简化了这些作品的制作。Collins的雕塑作品是用层板做出的，制作过程复杂而费时。因此，在动手制作最终的正式作品之前，Co11ins先用聚氯乙烯塑料管和蜂蜡片做一些样品。这一方法使曲面有精确的模型为依据，但它要花好几天的时间。为了加快制作速度，Sequin他的一位学生Houman Meshkin的协助下开发出一个制图程序．可以在计算机屏幕上显示Scherk-Col1ins曲面。

该程序使用户可以选择某些几何参数，这样艺术家在拉伸曲面或通过其它方式使曲面变形以寻找一种美观的形状时就有了相当大的自由。比较明显的参数是Scherk塔的层数以及扭转的程度，而其它一些参数则决定了比如说洞的大小等特性。Scherk塔本身也被推广了，引入了一些新的变种，例如把猴鞍面(而不是标准鞍面)连接起来所形成的Scherk塔。一旦在屏幕上做出了Scherk塔，就可以通过成型工具把虚拟雕塑转变为真实的作品。Sequin已经用这种方法创作出数十个Scherk-Col1ins曲面的模型。

然而，还存在一种更有争议的方案。现在计算机制图的功能已经非常强大，使虚拟雕塑可以制作得看起来几乎与真实雕塑完全相同。例如，制图软件可以使图像具有几乎任何一种表面质地，不论是有纹理的木材还是闪闪发光的铜、蜥蜴皮、布等等，总之你想要什么质地都可栩栩如生地显示出来。虚拟雕塑作品打印出的图像与真实作品的照片几乎无法区别。配备了虚拟现实头戴装置的艺术爱好者可以绕着虚拟雕塑作品细细观看，获得一种极为生动形象的三维感受。

既然如此，是否真的有必·要制作雕塑吗?难道不能让雕塑就一直保持虚拟的形式吗?对于这个问题，大多数传统的艺术家或许会作出否定的回答，但未来的艺术家——他们想必会相当熟悉虚拟现实系统的看法可能与之相左。Col1ins的态度是明确的：“人类已经进化到制造和使用工具，他们对人工创造的艺术伤口怀有美学上的深入感情，永远需要它们来揭示人们的本性。”换言之，虚拟的东西不能胜过真实的东西。