互动科普

中国的皇帝拥有不受任何制约的无限权力，砍人家的脑袋只要动一动嘴皮，易如反掌。唯一能使他们感到畏惧的只有玉皇大帝。古代的一则笔记小说上说，明太祖朱元璋晚年生性多疑，杀戮过度。有一天，天上突然响起了晴天霹雳，震坍了宫殿的一角，落地的雷火追杀朱元璋。他吓得面如土色，叩头如捣蒜，并连连向上帝谢罪，一面作出承诺：“陛下赦臣，臣赦天下”。从此以后，他就不敢乱杀人，比前期宽松多了。

上帝的鞭子

但是，在西方，居然有一位不怕上帝的人，那就是出生于1900年的犹太物理学家泡利(W．Pauli)，他被人们公认为“一代奇才”、世纪精英。

泡利一生对量子物理学作出了重大贡献，他提出的“不相容原理”堪称微观物理学的金科玉律，而“中微子假说”也是非常基本、非常独特的创见。

泡利为人不苟言笑，治学十分严谨。他批评起别人来不讲情面，不留余地，有时甚至要骂人“笨蛋”。然而泡利绝非学阀，作风也很光明磊落。他不大会处世，措辞也许不当，但动机很纯正，完全出于从严要求，一心为了学术研究。泡利由此而得了一个外号，叫做“上帝的鞭子”。

泡利对上上下下的各色人等都是一视同仁的，不仅对凡夫俗子，即便是至高无上的上帝耶和华，他也不肯卖帐。下面的一则脍炙人口的趣谈，足以略窥他的一贯作风。

精细结构常数(fine structure constant) 1／137出现于微观物理世界，先是在光谱理论中崭露头角，后来又在粒子理论中憧憧往来，它是一个没有量纲的纯数。泡利希望找到一种理论能自然而然地给出这个常数的值，可是他在有生之年却始终找不出什么线索，不免抱憾终身了。

按照天主教、东正教或基督教的教义，虔信上帝的好人死后，灵魂可以进人天堂，那时上帝就会满足他的一切愿望。据说泡利到了天堂以后，上帝和颜悦色地问他，打算要点什么好东西？他说别的事情都不想，只想知道精细结构常数为什么等于1／137。上帝听了此话，就给他几张纸片，说道：“答案就在这上面。”岂知泡利看了纸片上书写的东西之后，居然操着德语打官腔：“Dasist Falsch!”(这是错的) 好厉害的泡利，连上帝都得挨他的批评。怪不得人们听了这一半神话、一半寓言的幽默故事后，风趣地说：“泡利不光是上帝的鞭子，连上帝也吃了他一鞭子!”

一些蛛丝马迹

精细结构常数既然不带量纲，是个纯数，那么数学自然有权管它。起码它也是个“双重国籍者”，并不只是物理王国的子民。下面就从纯数学的角度，对它作一些探讨，首先是把各种性质收集起来。

分母137是个素数，它只能唯一地表示为两个平方数之和：137=16+121=4^2+11^2在137中，各位数字的立方和是1^3+3^3+7^3=1+27+343=371。

由此导出的371是个有名的“黑洞数”，因为按照下述的变换方法，371是不变的：3^3+7^3+1^3=371。

137这个素数，脾气有点怪，因为1／137在化成十进小数时，循环节只有8位(作为强烈对比，可以看到1／97的循环节长达96位)。

根据欧拉函数的理论，1／P的循环节的位数m应是满足下列同余式10m一1(modp)的最小正整数，而事实上10^8一1=99999999确实能被137整除。下表给出一些素数p的倒数的循环节。

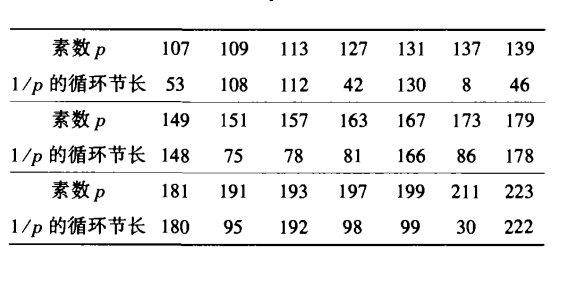
由此可见，在21个被调查的素数分母中，仅有p=137一例的循环节特别短，而其他素数分母的循环节都是令人可厌地冗长，可见137这个数确实有些凤毛麟角，与众不同，有它的独特之处。

更加令人注意的是1／137展成十进制小数时所表现出来的回文性质(palindromic property)：

1／137等于循环节为00729927的无限循环小数。

729927是个货真价实的回文数，从左至右读过去同从右至左读过来完全一模一样。

同号称“万物之灵”的人一样，回文其实是表现在语言、文字中的一种双侧对称(bilateral symmetry)现象，其中的微言大旨，颇有点耐人寻味了。

729927的素因子分解式为729927=32×11×73×101。其中有两个算式均可得出回文：729927÷73=9999；729927÷101=7227。另外73x137=10001，乘积是回文数，73与137这两个因子表面上看来虽非回文，但73与137耦连而成的73137却也是个回文数。

从1／137到136／137，这136个真分数的每一个都可以化成循环小数，其循环节一律都是8位，而且可以“一分为二”地分成前后两段，两段中对应数字之和都等于9。不妨随便举出一例：6／137=0．04379562，而0437+9562=9999。

轨道的探求

分数N／137(1≤N≤136)可以分成17个轨道(orbit)，也可以称为族(family)。而每个轨道由8个成员构成。17个轨道的推求方法基本类似，伤其十指，不如断其一指，只要把其中的一个轨道求出来，其他就不难“举一反三”地一一求得。下面就任择其中(选取是不抱偏见、完全任意的)之一来说说。

实际上，以下的八数可以构成一个轨道：

轨道中的各数均为无限小数但可以有限处理。从两个“能级”最低的成员出发，差为9489051—5109489=4379562，而4379562÷729927=6，得到的商恰为整数! 这就强烈地暗示了回文数729927的“量子”单位性质。

再看另一对，15／137与67／137之间为何要隔开这样长的一条“鸿沟”呢？

差为48905109—10948905=37956204，而37956204÷729927=52。结果竟然完全吻合，不亦快哉！

值得人们注意的是，如以1／137作为单位，则轨道八个成员之间的“级差”也表现了下列很奇异的回文对称性：

精细结构常数与量子论有关，而探索其秘钥时却用上了“量子”概念(尽管它是以数学形式出现的)，这倒是应验了一句老话“解铃还须系铃人”哩！

“精细”体现在哪里

“轨道”中各成员数之间的关系就像是节日(如正月十五元宵灯节)里常见的做成宫灯形状的“走马灯”一样：

怎样从“走马灯”的一态转成另一态呢，建议大家来做一个离经叛道的乘法(数字表面上很繁琐，其实不难。只要用一下CASIO计算器就行了)。10948905×8．26666666(乘数已用到七个6)=90510947．93。

干脆来个“一不做，二不休”，在末位按上八个6，此时就得出10948905×8．266666666=90510947．99。这就强烈暗示乘积应是不折不扣的整数90510948，不过此时已到了CASIO计算器使用功能的极限，九个6已经按不动，不起任何作用了！乘数必须是无限小数8．26666…(或简单地记为8．26)，才能天衣无缝地得出正整数90510948所谓精细，其微妙处原来就是无限与有限之间的矛盾统一与转化。

想要彻底揭开精细结构常数1／137的“自然之谜”，看来非得数学家与物理学家通力合作不可！