互动科普

    玻姆的量子力学替代理论

            David Z.Albert

这个理论在过去四十年的大部分时间里都被人们所忽视，它向量子力学标准理论所隐含的概率的、主观主义的现实性图景提出了挑战。

本世纪亚原子粒子行为的研究工作被认为是至少确定了关于现实世界的三个极其古怪的事实。第一个事实是，纯粹的偶然性支配着自然界最深层次的运行方式。第二个事实是，虽然物质实体总是占有空间，但是却存在它们并未占据特定空间区域的情况。第三个事实（或许是最令人吃惊的事实）是，支配着“寻常”物理实体行为的基本定律莫明其妙地完全无法适用于碰巧起“测量仪器”或“观测者”作用的实体。这些肯定是量子力学创立者们所确定的原则，后来则成为理论物理学的或多或少正式的定理，而今天所有标准教科书中关于这个问题都采用了上述说法。

但是目前正在出现的一个事实是那些结论确立得稍稍太快了一点。其实，存在着一种根本不同的、完全证明是有效的理论，它能解释亚原子粒子的所有已知的行为。在这个理论中，偶然性不起任何作用，并且每一种物质实体都必定占据着某一特定空间区域。此外，这个理论表现为一组基本物理定律，这些定律以完全同样的方式适用于所存在的每个物理实体。

该理论主要是伦敦伯克贝克学院已故的David J.Bohm（玻姆）的研究成果。虽然他的理论存在于科技文献中已达40多年，但是直到最近才受到人们重视。整个四十多年里，关于这类问题的见解一直受着标准定理支配，通常被称之为量子力学的哥本哈根诠释，因为它能或多或少地被追溯到丹麦物理学家尼尔斯·玻尔及其研究小组。

在本文中我将首先概述这个标准定理的主要论点，然后简要指出玻姆理论如何得以避开其中的一些论点。最后我将扼要介绍关于玻姆理论用何种方法和在何种条件下适合量子力学基本原则的现代思考。

使标准定理公式化的最简单方式或许与某些电子实验有关。这些实验都涉及到对通常称为电子自旋的两个分量的测定。为简单起见，我将把它们称作水平自旋和垂直自旋。

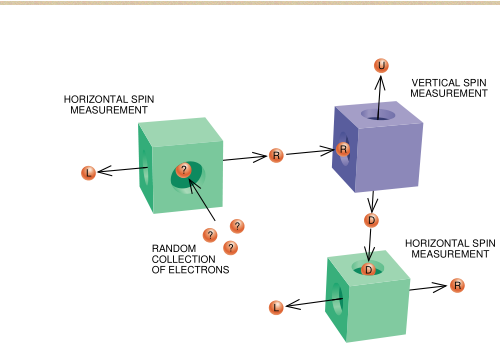
电子的水平自旋只能取两个可能值中的一个值碰巧是一个实验事实（就我们所知道的而言）。这种情况同样适合于垂直自旋。我将把水平自旋值称为右旋值和左旋值，并且将垂直自旋值称为上旋值和下旋值。

物理学家能采用现有技术轻易而准确地测定电子的水平自旋和垂直自旋。自旋测定装置的工作原理一般是根据其测定的自旋分量值来改变输送入该装置中的电子的运动方向。这样一来，那个自旋分量值其后便能通过对电子位置的简单测定而得以确定。我将把这些测定装置称为水平箱和垂直箱。

关于电子的另一个实验事实是，作为一种规则，在电子水平自旋值与电子垂直自旋值之间并不存在相关性。例如，输送进一个垂直箱入口孔的任一大群右旋电子中，恰好有一半电子（从统计学角度来说）将通过“上”孔冒出而另一半则通过“下”孔冒出这种情况同样适合于输入垂直箱入口孔的左旋电子，也适合于输送进水平箱的上旋和下旋电子。

关于电子的又一个实验事实，对于本文的目的而言是一个极其重要的事实，那就是对一个电子的水平自旋的测量能够干扰其垂直自旋值，反之亦然，而且这种情况的出现似乎是完全无法控制的。例如，如果人们对处于电子水平自旋的两次测量之间的任一大群电子的垂直自旋进行测定，那么始终将发生的情况是垂直自旋测量改变了通过它的电子的半数的水平自旋值，而另一半的水平自旋值却不被改变。

未曾有人设计出一种避免这类干扰的垂直自旋测量装置。此外，也未曾有人识别出这些电子群中的单个电子的任一物理性质，此性质能够决定其中哪些电子在测定垂直自旋的过程中其水平自旋值被改变，哪些电子则不被改变。

关于这些情况，公认的理论只能认为，就原则而言，不可能存在这样一种垂直自旋测量之类的过程，它除了对水平自旋值具有上述作用外还有其它任何作用。而且标准理论指出，电子的水平自旋在其垂自旋测量过程中被改变或不被改变只是一种绝对纯偶然性问题；支配着那些变化的定律完全不可能是确定性的。考虑到实验数据，这些结论似乎无疑是无害的和有道理的。

如果测量某种类型的自旋实际总是不能控制地干扰另一种自旋值，那么就不可能有办法同时确定在任何一个特定时刻时任何一个特定电子的水平自旋和垂直自旋的数值。这一现象是不确定性原理的一个实例：某些可测量的物理性质，例如位置与动量（在我们这个例子中则是水平自旋量和垂直自旋量），一般认为相互之间是不相容的。对其中—个的测量将总是不可控制地干扰对另—个的测量。许多其他已知的不相容的成对物理性质也存在这种情况。   

关于不可预测性就讲这么多。但是存在着更为捉摸不透的亚原子粒子特性。要显示它们将需要一种更为复杂的实验。设想一个测量电子垂直自旋量的箱子。上旋电子沿一条贴有向上标签的路径从箱子出来：下旋电子则沿一条贴有向下标签的路径射出。然后我们就能安排一对“反射墙”，使这两条路径在另一点上相交。这些反射墙表面可以设计为在任何方面都不会改变电子自旋特性。在两条路径相交的这个交叉点上我们放置一个“黑箱”，该黑箱将这两条路径合并为—条路径，而且也不会改变自旋值。

假定我们将一大群右旋电子一次一个地迭入垂直箱。这些电子沿中。然后当它们从黑箱出口冒出时，我们便测量它们的水平自旋量。我们预计将出现何种结果呢？先前的经验告诉我们，从统计角度看，这群电子中有一半将是上旋电子并且将占据通过该装置的向上路径，而另一半则将是下旋电子并且将占据向下路径。研究一下前一半电子。沿垂直箱和出口处之间的路径上没有什么东西能够对电子的垂直自旋值有任何影响。因而，它们将全部以上旋电子的形式从该装置出来。与我们先前得到的数据相一致，它们中有50％将是右旋电子，另外50％是左旋电子。下旋的那一半电子将具有完全相同的水平自旋统计量。将所有这些项期情况综合在一起，可得出结论：对于任何一组送入该装置的右旋电子，其中有一半被发现是右旋的，有一半是左旋的。

这些结果似乎绝对是顶先安排好的。但是当你实际去尝试这个实验时，一个有趣的情况发生了。最初被送入该装置的右旋电子（一次—个地，请注意）100％最后都表现为左旋。

将这—结果说成是现代物理学中最奇特的结果之—是一点也不夸张的。也许稍稍修改一下这个实验将会澄清—些问题。假设我们安装—面小型的活动电子阻隔墙，该墙能够任意地滑进滑出比方说向上路径中。当这堵墙滑出路径时，我们正好便有了先前的装置。但是当该墙滑进路径时，沿着上行路径运动的所有电子都被阻挡下来，并且只有沿着下行路径运动的那些电子得以通过而到达黑箱。

当我们滑入该堵墙时预计会发生什么情况呢？首先，黑箱出口处的电子总输出量应该下降50％，因为有一条路径被阻断了。剩下的50％的水平自旋统计量又如何呢？当该墙被滑出路径时最初送入的右旋电子100％地以右旋电子出现。即所有那些电子最后都是右旋电子，无论它们是占据上行路径还是占据着下行路径。于是，在上行路径上存在或不存在该墙都无法影响下行路径上的电子，所以剩余的50％电子应全是右旋电子。

正如我们可能已经推测的那样，在这个实验中实际上所发生的事情与我们的顶测值背道而驰。正如预计的一样，电子输出量减少了50％。但是剩余的50％并不都是右旋的。有一半是右旋的，而另一半是左旋的。如果我们反过来在下行路径中插入一堵墙，则会发生同样的情况。（熟悉量子力学的读者可能认识到这种实验是著名的双缝实验的一种逻辑上简化了的变型。）

人们能够如何理解这些实验所得到的结果与我们预期结果之间的不一致呢？研究一下墙从路径中滑出时通过该装置的—个电子。考虑一下关于该电子可能已取哪条路径的概率。它会取下行路径吗？很明显，不会取下行路径，因为取那条路径的电子（正如将墙滑入路径中的实验所揭示的一样）已知道具有50-50的水平自旋统计值，而在没有隔墙时通过我们装置的一个电子肯定被认为在装置出口处是右旋的。然后，它是否能取上行路径呢？由于相同的原因，它不能取上行路径。

它是否由于某种原因能够取两条路径呢？也不能。假设当某个电子正通过装置时，我们停止该实验并查看一下它在何处。结果证明有半的时间我们发现它处于上行通道并且在下行通路上根本没有电子，而有一半的时间我们发现它处于下行通路上，并且在上行通道上什么也看不到。它是否能两条通道都不用呢？肯定不会。如果我们在两条路径上都安上隔墙，则根本无任何电子通过。

看起来，某种非常深入的东西肯定会发生动摇。而事实上，这种情况的确出现了——至少根据已经成为过去半个世纪中理论物理学的中心原则中的一条原则（就是我在开始那一段中所提到的三个原则中的第二个原则，即关于位置不确定性的原则）。那个原则规定，这些实验使我们别无选择，只能认为电子取哪条路径通过这样一个奇妙装置的问题本身不具有任何意义。询问一个电子取什么路径被认为类似于（比方说）询问金枪鱼三明治的政治信念或5这个数的婚姻状况。人们认为问这样一些问题相当于误用语言，或者说相当于哲学家所谓的类别错误。

因而，物理学教科书关于这类电子的一般说法不是断然说这些粒子通过该装置时或者取上行路径或者取下行路径或者取两种路径或者两种路径都不取，而是说根本不存在它们取何种路径这样一个事实——不仅不存在已知的事实，而且是根本不存在任何事实。它们所处的状态是教科书中所谓的上行路径和下行路径的叠加态。

虽然这些观点大有悖于我们的直观感觉，大有悖于我们对物质和粒子的看法，但是一组简单规则已经被推导出来，它们在预言这些条件下的电子的所有被观测到的行为方面是非常成功的。此外，这些规则——当然被称为量子力学——已经证明在预言所有条件下所有物理系统的所有被观测到的行为方面是非常成功的。实际上，量子力学作为整个理论物理学的构架已有70多年的历史。

量子力学用来描绘物理系统的状态的数学对象被称之为波函数。在我已讨论过的这种单个粒子系统的简单情况中，量子力学波函数采取简单的位置函数的形式。例如，位于某一区域A的一个粒子的波函数将在除A之外的空间中的任何地方具有零值而在A中将具有非零值。与此类似，位于某一区域B中的粒子波函数将在除B之外的空间的任何地方具有零值而在B区域中将具有非零值。而处于区域A和区域B的叠加态的一个粒子的波函数——例如恰好才通过垂直箱的—个最初为右旋的电子的波函数——将在这两个区域中具有非零值而在其他任何地方则具有零值。

量子力学的一条最重要规则（玻姆理论将明确地违反这条规则）就是用渡函数表示物理客体就等于完全描述了这些客体。它指出在任何给定瞬间对任何—个给定的物理系统的任何描述都能够从其波函数中推出。

物理学定律的内容——实际上，根据量子力学即物理学定律所能够包括的所有东西，以及物理学定律将要包括的所有东西——就是物理学系统的波函数如何随时间演化。量子力学教科书提到这类定律的两种类型。这一理论的特别独特的地方在于，当上述那些物理学系统未被直接观测到时，其中一种类型适用，而当它们被观测到时，则另一种类型定律适用。

第一类定律通常以线性微分“运动方程”的形式表示。例如，它们要求送入垂直箱的—个初始右旋的电子将以沿上行路径运动和沿下行路径运动的叠加形式从箱子中出来。此外，所有可获得的实验证据都指出，那些定律支配着每个单个孤立微观物理系统在所有条件下的波函数。于是，由于微观系统是存在着的每一事物的组成部分，所以乍看起来可能会有较好的理由假定那些线性微分方程是整个物理学宇宙的真正的运动方程。

但是，如果波函数实际上是物理学系统的完整描述（正如量子力学所坚持认为的那样），那么此结论就不可能是完全正确的。首先，由那些方程表述的定律是完全确定的，而纯偶然性的因素看起来在自旋箱的实验的结果中起了一种作用。

研究一下起初处于区域A和区域B的叠加态的一个电子的位置的测量结果。简单的计算揭示，线性微分运动方程提供了关于这样—种测量过程的结果的明确预测。然而，那些方程并未预测测量装置可能会或者指出在区域A中发现这个电子或者指出在区域B中发现这个电子（这是当你实际进行类似测量时所发生的情况）。相反，那些方程却认为测量装置肯定最终会达到指出在区域A中发现这个电子和指出在区域B中发现这个电子的叠加状态。换一种稍稍不同的说法，那些方程预测，测量装置最后可能会达到一种物理学状态，在这种状态中，完全不存在关于它正在指出的东西的事实。几乎不需要提到，这样一些叠加状态（无论它们是什么）不会正确地描述当你实际进行这样一种实验时将会得到什么结果。

因而，根据公认的推理，第一类定律必须补充以第二类定律，后者将明显是随机的。例如，它要求，如果要测量开始时处于区域A和区域B的叠加态中的一个电子的位置，那么可能会有50％的概率在区域A发现那个电子和50％的概率在区域B中发现那个电子。换句话说，如果这个电子的位置被测量，则可能会有50％的概率在电子的测量过程中使波函数的值在区域A之外任何地方变为零，且有50％的概率在电子的测量过程中使波函数的值在除区域B之外的任何地方变为零。（这种改变有时被称为波函数的“坍缩”。）

人们如何区别第—类定律运用的条件与第二类定律运用的条件呢？量子力学的创始人所要说的一切就是，它与“测定”和“普通物理过程”之间的区别有关，或者说它与观察者和被观察者之间的区别，即主体与客体之间的区别有关。

一些时候以来，许多物理学家和哲学家都认为这一状况是非常不能令人满意的。看起来可笑的是，自然界的最基本定律的最好的现有理论竟然依赖于这样一些不明确的和难以捉摸的区别。消除或者改正这种不准确性的复杂而艰难的任务在过去三十年里已经成了量子力学基础的中心任务。它有这样一些名称，如薛定谔的猫问题，或维格纳的朋友问题，或量子态衰减问题等。我将用最普遍的当代名称来称呼它：测量问题。

测量问题的一个特别惊人的解决办法是由美国出生的物理学家David J．玻姆发明的。法国物理学家德布罗意早几年提出了一个相近的方案，但是德布罗意的方程却没有玻姆的方程那样通用和有效。后来，已故的物理学家John Bell将玻姆的最初理论改写成为一种非常简单和令人信服的形式。

玻姆的理论设想粒子是必定位于—个或另一个特殊地点的一类事物，尽管前面提到的所有证据均与这一说法相矛盾。此外，关于世界是由什么构成的，玻姆理论比哥本哈根诠释更为明确得多。在玻姆的解释中，波函数不仅仅是数学客体而且是物理客体，即物理事件。玻姆将它们处理为稍稍有点象经典力场。例如引力场和磁场。在玻姆理论中波函数的作用（就象经典力场的作用一样）实际上就是把这些粒子推来推去。引导它们沿着它们的合适路径运动。  

支配波函数随时间推移而演变的定律被准确地规定为标准线性微分量子力学运动方程一但是这次无论什么都没有例外。在玻姆理论中已有其他定律规定这些波函数如何推动它们各自的粒子运动。所有这些定律都是完全确定的。因而，在任何时候世界上所有粒子的位置。以及在那个时候世界的完整量子力学波函数，都能根据任何较早时候世界上所有粒子的位置和世界的完整量子力学波函数确定地计算出来。

不能进行那些计算以及在那些计算结果中的任何不确定性，必定是这个理论中的一种认识上的不确定性。它仅仅是无知的问题，而不仅仅是世界基本定律中任何不可分的偶然性因素的作用。尽管如此，这种理论仍然要求对于我们原则上存在着这样一种无知。玻姆理论的运动定律确实将这种无知强加于我们，对于重现量子力学的统计学预测来说，这种无知已被证明是恰好足够，并且恰恰是我们所需要的那类无知。它依靠的是对人们尚不知道的过程的一种平均作用，而且正好是在经典统计力学中起作用的那种平均。

这个理论描述一种真实的、具体的和确定性的物理过程——即一种能够以精确数学细节加以描述的过程——而测量行为则不可避免地阻碍了正在加以测量的东西。换句话说，玻姆理论要求，这类无知——虽然它仅仅是关于完全明确的事实的无知——不可能在不违反物理定律的情况下被消除掉。

玻姆理论能完全解释两条路径装置的实验结果——这些实验似乎意味着电子能够处于一些不存在关于它们在哪儿的事实的状态中。在初始右旋电子送入这种装置的场合，玻姆理论要求电子或者将取上行或者将取下行