互动科普

螺旋粘霉菌

Lan stewart

2O00年的夏天，我参加了在葡萄牙举行的一次关于模式形成的数学原理的会议，其中一位发言者的演讲使我想起了我第二喜欢的一种动物。我最喜欢的一种动物是老虎，其原因之一是因为我喜欢老虎那一身有着漂亮条纹的毛皮。我第二喜欢的生物也是因为它的条纹使我感兴趣，但这种生物赶不上老虎那么威武,这种生物就是粘霉菌。更具体地说就是细胞粘性霉菌中的一个种属，名由Dietyosteliuma~seoideum。

生物学家发现粘霉菌令人着迷，因为它是介于单细胞原生动物和多细胞生物之间的一种生物。粘霉菌也揭示了人类基因组的探索者应牢记在心的一个生物学真理：重要的不仅仅是你的基因，而且是你如何对待这些基因。尽管粘霉菌在生命树中的地位很低，但它是创造出了漂亮得惊人的螺旋形图案。这些图案在多大程度上由粘霉菌的基因编码呢?事实上,是否存在着螺旋形基因?

为了回答这个问题，我们需要了解粘霉菌是如何形成螺旋形图案的。螺旋形图案实际上是集体活动的成果,粘霉菌的生命周期始于一种随风到处飘荡的微小的孢子。如果该孢子恰好遇到一处适宜的潮湿落脚地，它就会长成一只单细胞的阿米巴菌并开始搜寻食物(主要是细菌)当这只阿米巴菌长到足够大后．它就通过一分为二的方式进行繁殖，很快就会出现许许多多的阿米巴菌。

当食物趋于短缺时，螺旋形图案就开始出现了，这时阿米巴菌就会集成团,而在它们向一团的中心移动的过程中，有时就形成漂亮的螺旋形。群聚的阿米巴逐渐变得越来越密集，而螺旋形也就卷得越来越紧。到某个时候，螺旋形就分裂成一种流动形(streamingpat),看起来就像从中心向外扩展的根或树枝流线逐渐变粗，而随着越来越多的阿米巴菌争嚣进入同个位置，它们就堆聚起来成为所谓的slug(要与名字相同的软体动物蛞蝓搞混)。

Slug是一群阿米巴菌，但它就一个单独的生物体那样运动，一旦它找到一处干的地方,它就牢牢附在地上,竖起来成为一根长长的茎，在茎的顶端是一团圆圆的东西,称为‘结实体’(fruitingody)，结实体中的阿米巴菌变成孢子随风被吹走,从而开始新的一轮生命周期。

柏林洪堡大学的生物物理学家Thomas Hofer发现了一个简单的机制，能够复现粘霉菌形成的螺旋形图案和流线形图案。邓迪大学的Comelis J. Weijer证明“方程能够模拟Slug的运动”。决定图案形状的主要因素是阿米巴群体的密度、阿米巴菌产生一种名为M环状腺瞟岭核苦酸(Cyclic AMP)的化学物质的速率以及各个阿米巴菌对这种化学物质的敏感度。大致说来就是每只阿米巴菌通过发出Cyclic AMP的喊叫声而向它的邻居们显示它的存在，然后阿米巴菌就向它喊叫声最响亮的方向移动,螺旋形图案是这一过程产生的一个数学结果，当位于群体中心他的阿米巴菌随着它们向外发出一波又一波的Cyclic AMP而转动时螺旋形图案就形成了。

因此,看来粘霉菌的大多数基因都只是告诉粘霉菌如何变成一只阿米巴菌，这些基因告诉细胞如何发出化学信号、如何感知化学信号以及如何应答化学信号。但是它们产生的螺旋形图案并不是受基因支配的。螺旋形图案产生于阿米巴菌所服从的数学规则，教学特性对于确定粘毒菌的生命周期可能起到了和遗传特性一样大的作用。

得出这一具有深远影响的(同时也是有争议的)结论的方程是将近50年前英国数学家阿兰·图灵提出的若干方程的修正形式(阿兰·图灵最有名的成就是同其它学者一起开创了计算机科学)。图灵也对形态发生(即生物组织与器官的形成和分化)感兴趣。1952年他提出一个猜测:生物体中的有序模式并不需要一个有序的前体。他认为,模式可能生于一类称为“morphogen”的化学物质，这些化学物质在穿过组织时彼此发生化学反应。

当图灵首次公开他的这设想时，它们还只是纯理论的东西，但是”图灵图案”的一个引人注目的实例很快就出现了：Beloi1sov—Zhabotinsky(BZ)化学反应。俄国科学家B．P. Belousov(随后是他的问胞A．M．Zhabofinsky)发现，petri氏碟中把几种通常的化学物质(包括溴酸钠、硫酸和malonic酸等)混合在一起，将会产生与粘霉菌产生的图案极为相似的同心圆环和螺旋形类似的反应，还可以产生条纹、斑点、花纹以及动物世界巾常见的其它许多种图案。

但是生物学家们拒不接受图灵的想法。图灵理论存在的一个主要的问题是，在BZ反应中自发产生的图案不是固定的，它们将穿过petri碟运动。化学家们观察到的其它所有图灵图案均是如此。而大多数生物的图案都是固定的，谁也没见过斑马的条纹或豹的斑点在它们身上动来动去。图灵从理论上证明来他的方程既能产生静止的图案，又能产生运动的图案。但是实验室中进行的试验似乎只产生运动的图案。后来,化学家们发现了其中的奥妙：如果在凝胶中不是在液体中进行反应，那么所产生的图案就是静止的。生物体应该与凝胶而不是与液体更相似。但到人们弄清楚这一区别时,生物学家已对这场争论不再感兴趣了。

不过数学家仍在继续思考图灵的设想,虽然他的方程过于简单,不能模拟精致的生物现象，但它们却的确产生了通常动物身上看到的那一类图案。如果按照波的波峰与波谷的位置加上不同的色彩，你就得到了条纹。更复杂的则可以产生斑点。数学家们面临的挑战是要利用能够更加真切地模拟生物学机制的理论模型来充实图灵的想法。

1995年，两位日本科学家发现了生物图灵图案的第一项有说服力的证据。京都大学的ShigeruKondoll RihitoAsai对成长中的扁鲛进行了几个月的观察，注意到它们身上的条纹在逐渐重新排布。在哺乳动物身上,毛皮的图案是随着动物的生长运渐变化，但是发育中的扁鲛却随着条纹的一分为二而不断形成新的螺纹。而且，这种变化可以用非常类似图灵方程的数学方程来加以预测。对一维细胞条纹的移动相当慢，因此,我们通常不会注意到。但正如伽利略所说，不管怎么说它还是在运动数学改变了扁鲛的外观。正如它影响着粘霉菌的——或许有我们自已的——生命周期一样。

郭凯声／译     向俊／校

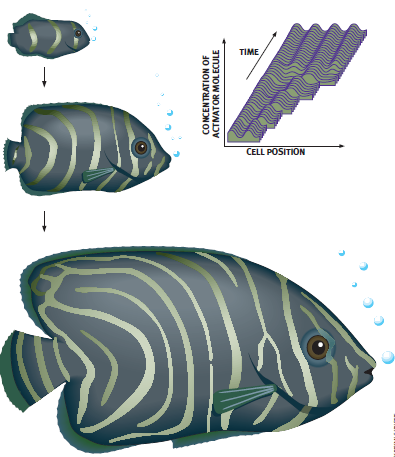
1、变化多端的扁鲛在发育成熟的过程中产生出新的条纹图案在(右上图)这一过程的计算机模拟中，波峰相当于条纹。

2、如这幅画家的作品所示一个粘霉菌群落中机灵的阿米巴菌形成了螺旋形图案。