互动科普

耦合振荡子与生物同步

Steven H．Strogatz，Ian Stewart

一条微妙的数学线索将时钟、缓步行走的大象、大脑节律及混沌的发生等联系起来。

1665年2月，伟大的荷兰物理学家、摆钟的发明人克里斯蒂安·惠更斯因患了一点小病而赋闲在家。一天，由于无所事事，他无意识地盯着他不久前刚造好的两台并排挂在一起的时钟。忽然间他注意到一件奇怪的事情：两个钟摆的振荡是完全同步的。

他用了好几个小时观察这两台钟，然而钟摆的节奏从未乱过。后来他试图打乱其节奏，然而不到半小时钟摆又恢复同步摆动了。惠更斯猜测这两台钟必定通过某种方式相互影响——或许是通过微弱的空气运动或它们的公共支撑的无法觉察到的振动。果然，当他把这两台钟分别移到房间的相对两侧

后，它们的摆动便逐渐不同步了，一台钟比另一台钟每天慢5秒。

惠更斯的这一偶然发现开辟了整整一个数学分支：耦合振荡子理论。自然界中耦合振荡子随处可见，但在生物中尤其显著：心脏中的起搏细胞；胰腺中分泌胰岛素的细胞；以及大脑和脊柱中负责控制有节律的动作——如呼吸、跑步和咀嚼等——的神经网络；事实上，并不是所有的耦台振荡子都必定局限于同一个生物体内，看看许多蟋蚌齐声鸣叫以及无数的萤火虫同步发光的情形就可以知道。[参见《科学美国人》1976年5月号上的“Synchronous Fireflies”一文。]

自从1960年左右起，数理生物学家们就一直在研究简化的耦合振荡子模型，这些模型保留了其生物原型的实质要素。过去几年中由于计算机和计算机制图学领域获得的突破，数理生物学家与乐于接受理论的实验工作者进行的合作研究，从物理学中借用的概念以及数学本身的新成就等，这方面的研究取得了迅速的进展。

为了认识耦合振荡子是如何协调工作的，首先必须了解一下振荡子是怎样单独起作用的。任何显示周期性行为的系统都是一个振荡子。例如，钟摆在摆动时每隔一定的时间就回到空间的同一点上；此外，它的速度也是极有规律地增加和减少。

数学家们并不只是从时间的角度来考虑振荡子的行为，他们也对振荡子在相空间中的运动感兴趣。相空间是一种抽象空间，它的坐标描述了系统的状态。例如，在不同的高度上把摆松开，并给出其位置和速度图，便可画出摆在相空间中的运动。相空间中的这些轨迹呈闭合曲线的形式，因为同其他任何一种振荡子一样，摆总是一再重复相同的运动。

单摆由一个重物挂在一根系索的端部而构成，这种摆可以取相空间中的无穷多个闭合路径中的任何一个，具体的路径由摆被松开时所处的高度而定。相比之下，生物系统(以及钟摆)，通常不仅有特征周期，而且也有特征振幅。它们在相空间中画出一条特定的路径；如果有某种扰动迫使它们脱离了

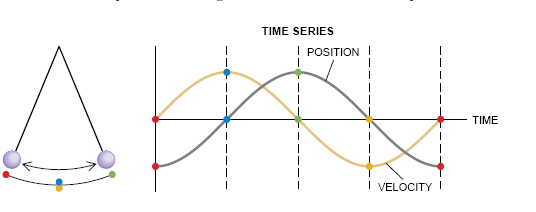
其已习惯的节律，它们很快又会恢复到其先前的路径上。假如某人使你吓一跳(比如说大喝一声“呸!”)，你的心脏可能会开始咚咚直跳，但很快它就会放松到其正常状态。

具有标准波形和振幅，在受到小的扰动后又很快恢复到这一标准波形和振幅的振荡子称为极限环振荡子(limit-cycle oscillator)。极限环振荡子具有

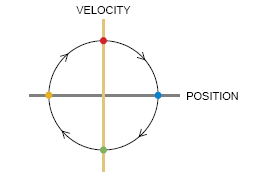
一种耗散机制，并有一个能源；当振荡变得过大时，耗散机制对振荡起阻尼作用，而当振荡变得过小时，能源就为振荡提供能量。

单个振荡子在相空间中画出一条简单路径。但是，当两个或两个以上的振荡子发生耦合时，其可能行为的范围就复杂得多了。支配其行为的方程一般是无法解出的。每个振荡子可能仅与靠得最近的几个振荡子发生耦合(如小肠中的神经肌肉振荡子那样)，也可能与一个巨大群体中的所有振荡子发生耦合。数学家们认为最容易描述的情况，是每个振荡子均影响系统中的其它所有振荡子，且耦合力随振荡子之间的相位差的增加而增大。在这种情况下，处于同步运动的两个振荡子之闻的相互作用为最小。

事实上，同步是耦合振荡子的最为人们所熟悉的组织模式。这类耦合的最壮观的例子之一可以沿着马来西亚、泰国和新几内亚的潮汐河观察到。在这些河边，成千上万只雄性萤火虫夜间聚集在树上，同步闪亮又同步熄灭，以吸引在它们头顶上游荡的雌萤火虫。当萤火虫在黄昏到达河边时，它们的闪亮并不是同步的。随着夜色加深，一团团同步发亮的萤火虫开始出现并不断扩大。最终整棵整棵的树步调整齐地忽亮忽灭，构成一幅持续数小时的无声的使人昏昏欲睡的图景。

奇怪的是，虽然萤火虫的求偶夸耀行为显示了规模壮观的偶合振荡，但这一行为的细节长期以来一直无法用数学方法进行分析。萤火虫是“脉冲耦合”振荡子系统的典型：仅当一只萤火虫看见另一只萤火虫突然闪亮并相应地调整自己的闪亮节奏时，萤火虫之间才发生相互作用。脉冲耦合在生物学中很普遍——请看看齐声呜叫的蟋蟀或通过所谓“动作电位”的电脉冲信号互相通信的神经元——但是这种耦合的脉冲特性很少被纳入数学模型中。由

于脉冲耦合将间断行为引入了一个在其它方面均是连续的模型中，从而使绝大多数标准的数学方法无法运用，因此它很难用数学方式处理。

本文作者之一(Strogatz)最近同波士顿学院的Renato E．Mirollo一起创立了—个关于萤火虫和其它脉冲耦舍振荡子系统的理想化数学模型。我们证明了，在一定的条件下，在不同时刻开始振荡的振荡子最终总是变成同步振荡。[见本期“业余科学家”专栏文章“电子萤火虫”。]

我们的研究工作得自于纽约大学的Chades S Peskin的一项较早研究的启发。1975年，Peskin提出了心脏的天然起搏器——即由大约一万个细胞构成的一个称为窦房结的细胞群——的高度概括的模型。他希望解决这些细胞是如何使它们的电节律保持协调一致以产生正常心搏的问题。

Peskin用一大批相同的振荡子来模拟这个心脏起搏器，每个振荡子均以同等强度与其它所有振荡子相耦合。每个振荡子都以一个电路为基础，此电路由一个电容器与—个电阻器并联而成。—个恒定的输入电流使电容器两端间的电压逐渐增加。当电压上升时，流经电阻器的电流量也增加，因而增加的速度逐渐下降。当电压增加到一个阈值后，电容器就放电，电压一瞬间就降到零——这一过程很象心脏起搏细胞的激发及其随后返回到基线的过程。然后电压再次上升，这一循环过程又重新开始。

Peskin的模型的一个突出特点是它代表了一种生理学上可能的脉冲耦合形式。每个振荡子都仅在激发时才影响其它振荡子。它使其电压增加一个固定的数值，如果任何细胞的电压超过了阈值，它就会立即激发。根据这些规则，Peskin陈述了两个颇令人感兴趣的猜想：第一，这个系统最终总是要变成同步的；第二，即使振荡子不是完全相同，这个系统也将变成同步。

当Peskln试图证明他的这两个猜想时，他遇到了技术性的障碍。那时不存在处理任意大的振荡子系统的成熟的数学方法。因此他退而求其次，将注意力集中在最简单的情形上，即只考虑两个完全相同的振荡子。即使对于这个问题，其数学方法仍是很棘手的。因此他又对问题作了进一步的限制——仅允许有无穷小的脉冲，穿过电阻的泄漏也为无穷小。至此这个问题才得以解决了。对于这一特殊情形，他证明了他的第—个猜想。

Peskin的证明依赖于二十世纪初期杰出的法国数学家Henri Poincaré提出的一个设想Poincaré的这一设想相当于数学上的频闪摄影术。取两个相同的脉冲耦合振荡子A与B，并在A一闪亮时就给它们拍一幅快照，由此给出其演变情况。

这一系列快照看起来象什么样子呢？振荡子A刚激发过，因此它始终处于电压为零的状态，而振荡子B的电压在各幅快照间则不相同。Peskin在解出他的电路方程后，发现了一个用于计算各次快照间振荡子B的电压变化的复杂的显式公式。此公式表明，如果电压低于某一临界值，则它将持续减少直至达到零：而如果它高于这个临界值，则它将增加。无论是哪种情况，振荡子B最终都将与振荡子A同步。

有一个例外情况：如果振荡子B的电压恰好等于临界电压，则它就既不能升高也不能降低，于是就一直处于临界状态。这两个振荡子反复地在彼此的相位相差半个周期的情况下激发。但是这—平衡态是不稳定的，就象把一支铅笔笔尖朝下竖起来放立一样。只要受到极轻微的扰动，这个系统就会趋向于同步状态。

虽然Peskin成功地分析了两个振荡子的情况，但是任意多个振荡子的情况在长达15年的时间里仍无法证明。1989年，Strogatz在亚利桑那大学的Arthur T．Winfree所著的一本关于生物振荡子的著作中获知了Peskin的研究工作。为了得到对Peskin的模型的行为的直观认识，Strogatz编写了一个计算机程序以对任意数目的相同振荡子，任意的脉冲尺度和任意的泄漏量来模拟这一行为。结果是很明确的：系统最终总会达到同步激发的状态。

在计算机模拟结果的鼓舞下，Strogatz与Mirollo讨论了这个问题。他们检查了Penskin对两个振荡子的情况的证明，并注意到采用一种更抽象的单个振荡子模型就可以澄清这一问题。此模型的关键特征原来是电压(或电压的等价量)在增加到接近激发阈值的过程中的逐渐减慢的上升曲线。其它特征是无关紧要的。

Mirollo和Strogatz证明了，对于任意数目的振荡子以及几乎所有的初始条件，他们的推广了的系统终将变成同步。这一证明基于“吸收”的概念。(吸收是对这一现象的概括：如果一个振荡子使另一个振荡子超过了阈值，则它们将永远保持同步。)毕竟这些振荡子有相同的动态特性，且以相同的方式与其它所有振荡子耦合。Mirollo和Strogatz得以证明，一系列的吸收最终将把所有振荡子锁定在一起。

虽然同步是互相耦合的同种振荡子的最简单状态，但它并不是不可避免的。事实上，耦合振荡子常常不能达到同步，其原因在于所谓“对称破缺”的现象。这一现象就是单个的对称态——例如同步一一被若干个对称性较差，但合起来却代表了原先的对称性的状态所代替。耦合振荡子是对称性破缺的一个丰富的来源。

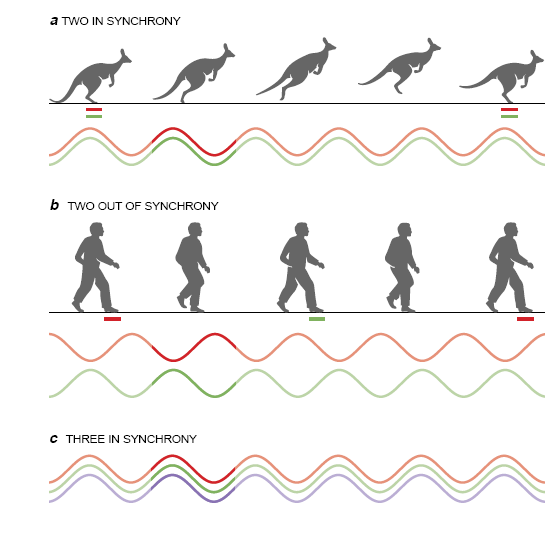
同步是所谓相位锁定这一普遍效应的最明显的一种情况。相位锁定就是许多振荡子画出同样的图形，但不一定是同步的。当两个相同的振荡子耦合时，恰好有两种可能情形，一种情形就是同步，即相差为零，另一种是反同步，即相位差为半个周期。例如，当一只袋鼠在澳大利亚的内地跳跃时，它那强壮的后腿作周期性的振荡，且两条腿在同一瞬间着地。与此同时，当一个人在追逐袋鼠时，他的双腿是交替着地的。如果网络有两个以上的振荡子，可能情形的范围便会扩大。1985年，本文作者之一(Stewart)与休斯敦大学的Martin Golubitsky合作，根据马里兰大学的James C．Alenxander和休斯敦大学的Giles Auchmuty的更早的研究成果，得出了一种对耦合振荡子网络的模式进行分类的数学方法。

该分类法是群论(群论处理若干对象构成的集合的对称性)和Hopf分岐(对振荡子“启动”方式的广义描述)相结合的产物。1942年，Eberhard Hopf确立了对振荡的起始的一般描述。开始时他考虑在相空间有一个休止点(即定常状态)的系统，并观察在用—个简单的线性函数来近似描述它们在休止点附近的运动时会出现什么情况。当系统逐渐远离休止点时，描述某些系统的方程显示出相当奇特的行为。它们既不缓慢地返回平衡状，也不会迅速地向外运动而进入不稳定状态，而是发生振荡。发生这一转变的点称为分歧点，因为系统的行为在此分为两个分支——一个不稳定的静止态与一个稳定的振荡态共存。Hopf证明了其线性化形式经历这类分歧的系统是极限环振荡子：它们有一个优先波形和振幅。Stewart和Golubitsky证明，Hopt的设想可以扩展到相互耦合的同类振荡子系统，这类系统的状态经历分歧而产生标准的相位锁定模式。

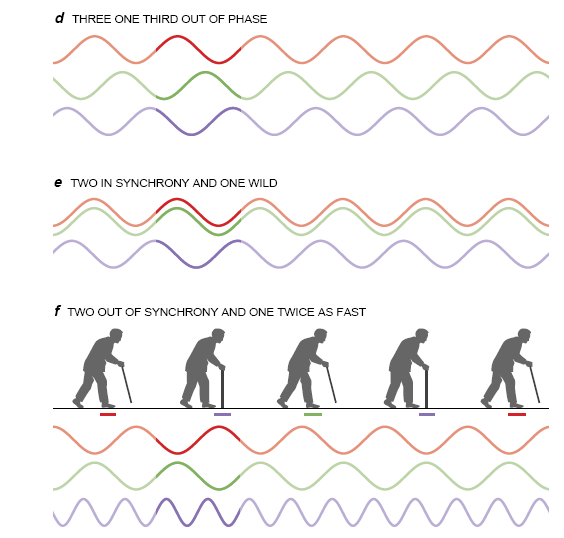
例如，在一个环中耦合的三个相同的振荡子，其相位锁定有四种基本模式：1．所有振荡子同步运动：2．振荡子相继绕环运动，其相位彼此相差1／3个周期；3．两个振荡子同步运动，而第三个的运动方式则与它们无关(除了其振荡周期与另外两个振荡子相同以外)：4．两个振荡子的运动相差1／2个周期，而第三个振荡子的振荡频率则是这两个振荡子的两倍。

第四种模式中出现的奇特的半周期振荡最初令人感到意外，甚至连Stewart和Golubitsky也是如此，但事实上这种模式存在于实际生活中。拄着一根拐杖行走的人，其行走的方式正是如此：先是右脚着地，接着是拐杖着地，然后是左脚着地，如此重复下去。在某种意义上，第三个振荡子是由另外两个振荡子的联合作用所推动的：每当这两个振荡子中的一个达到其峰值时，它就对第三个振荡子产生推动作用。由于头两个振荡子是精确地反同步的，因此当另外两个振荡子每个达到其峰值一次时，第三个振荡子就两次达到峰值。

借助于对称Hopf分歧的理论，可以对许多不同的耦合振荡子网络进行相位锁定模式的分类。事实上，Stewart与波士顿大学的生物医学工程师James J．Collins合作，一直在研究相位锁定的这些模式与动物的步法(如小跑、溜蹄、疾驰等)之间的明显相似性。

四腿行走的步法与四振荡子系统的自然模式非常相近。例如，当一只兔子跳跃时，它先使其前腿一齐运动，接着使其后腿一齐运动。两只前腿间的相位差为零，而前腿与后腿间的相位差为1／2个周期。长颈鹿的溜蹄也与之类似，但此时长颈鹿的每一侧的前腿和后腿一齐运动。马在小跑时，其步法

的相位锁定呈对角形式。大象在慢步行走时轮流抬起每一只腿，每一阶段上的相位差均为1／4个周期。小瞪羚的步法是这一对称集合中的最后一种，即四脚齐跳，也就是所有的脚都保持同步运动[见《科学》1991年第8期的“数学游戏”专栏文章。]

后来，Steward和Collins把他们的分析扩展到了昆虫的六脚运动上。蟑螂的三脚步法是6振荡子环中的一种非常稳定的模式。构成一个三角形的三只脚——左前脚、左后脚和右中脚——同步运动，然后是另外三只脚一齐抬起，它们与前面三只脚的相位差为1／2周期。

为什么步法会这样类似于耦合振荡子的自然模式呢?动物四肢的机械布局不大可能是其主要原因。四肢并不是无源的机械振荡子，而是由骨骼和神经组成的复杂系统，它们由同样复杂的神经系统加以控制。自然现象和数学结果间的这种一致，其最可能的起源在于控制运动的神经系统电路的结构。生物学家很久以来就猜想存在着一类被他们称为中央模式发生器的耦合神经元网络，但是这一假说一直是存在争议的。不过，神经元的行为常常类似于振荡子，因此，如果中央模式发生器存在的话，人们就有理由期望其动态特性类似于振荡子网络的动态特性。

此外，对称性分析解决了中央模式发生器假说中的一个具有重大意义的问题。大多数动物都有几种步法，例如，马可以慢走、小跑、慢跑、疾驰等，而生物学家们则常常假定每种步法都需要一个单独的模式发生器。但是，对称性破缺意味着同一个中央模式发生器电路可以产生动物的所有各种步法。只有神经振荡子之间的耦合强度需要改变。

至此我们的分析仅限于所有振荡子完全相同的振荡子集合。这一理想化假设在数学上是很方便的，但是它忽略了生物学中始终存在的多样性。在任何一个真实群体中，某些振荡子总是天然地就比其它振荡子快一些或慢一些。其成员具有不同的振荡频率的振荡子群体的行为取决于它们之间的耦合强度。如果振荡子的相互作用太弱，它们就不能达到同步，其结果就是得到不协调的振荡。这样的振荡子即使从同步状态开始，也会逐渐变成异步，正如惠更斯的摆钟放在房间的相对两端后所发生的情况那样。

一种生物发光藻类(Gonyaulax)的群落显示的正是这种失同步过程(desynehronization)。哈佛大学的J．Woodland Hastings及其同事发现，如果让装满Gonyaulax的水箱保持在实验室的微弱光线照射下，它就显示出一种生理节奏性的发光节律，其周期将近23小时。随着时间的推移，波形开始展

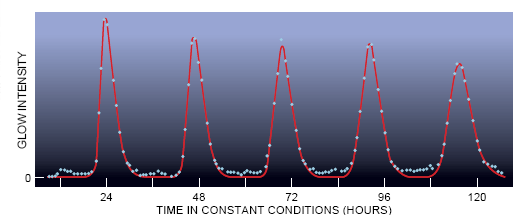
宽，这一节律就逐渐消失了。看来各个细胞仍在继续振荡，但是由于其固有频率的差别，它们逐渐变得不同步。如果没有日光的照射，这种藻类本身的发光不会保持同步。

在其它一些振荡子群体中，耦合强度大到足以克服固有频率的差别。五十年代后期，Polymath Norbert Wiener指出，这类振荡子群体在生物学(事实上是在整个自然界中)随处可见。Wiener试图弄出一个关于振荡子集合的数学模型来，但是他的方法已被证明是不很成功的。后来，在1966年，当普林斯顿大学的一位研究生Winfree开始研究极限环吸引子的大群体的行为时，理论上的突破出现了。他颇有灵感地将计算机模拟、数学分析和实验结合起来，以用于研究一个由71个电耦合霓虹管振荡子阵列。

Winfree指出，如果振荡子是弱耦合的，则它们将一直接近其极限环，这样他就使问题得到了极大的简化。这一深刻认识使他能够忽略振幅上的差异，而只考虑振荡子的相位上的差异。为了把振荡子间的差别考虑进去，Winfree建立了一个模型。他假定振荡子的固有频率的分布服从一个狭窄的概率函数，且假设振荡子在其它方面都是相同的，这样他就使他的模型抓住了振荡子群体的实质所在。他作的最后一步，也是至关重要的一步简化，就是假定每个振荡子都仅受其它所有振荡子产生的集体节奏的影晌。例如，对萤火虫来说，这就意味着每只萤火虫都是对整个萤火虫群体的集体发光作出应答，而不是对任何的单个萤火虫作出应答。

为了直观化地表示Winfree的模型，试设想许多个点围绕一个圆在运动。这些点代表振荡子的相位，而圆则代表其共同的极限环。如果这些振荡子是相互独立的，则所有的点最终将分散在整个圆上，集体节律将削弱到不复存在。此时是不和谐占了统治地位。然而，一条关于振荡子问相互作用的简单

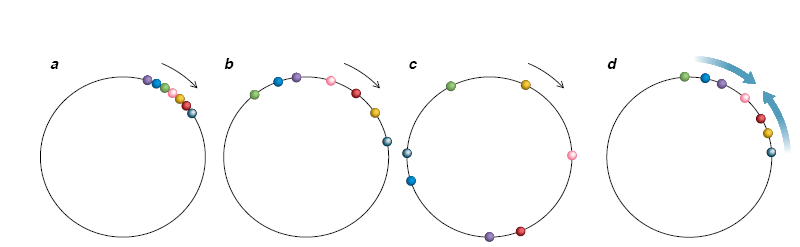
规则可恢复同步，这条规则就是：如果—个振荡子跑到了群体的前面，就使它的速度放慢一点，而如果一个振荡子掉在了后面，就使它的速度加加快一点。

在某些情况下，这一集体耦合能够克服固有频率的差异；在另外—些情况下则不能。Winfree发现这个系统的行为取决于频率分布的宽度。如果与耦合相比频率的展宽很大，那么这个系统终将进入不同步状态，就好象它根本没有耦合一样。当频率展宽减小到一个临界值以下时，该系统的一部分就会自发地“冻结”到同步状态。

同步是通过合作实现的。如果有少数几个振荡子碰巧处于同步状态，则它们的同步信号联合起来就可能超过背景噪声，从而对其它振荡子施加更大的影响。当更多的振荡子被拉入同步核中时，它们就进一步加强了同步核的信号。这一正反馈导致同步的加速出现。但是有些振荡子却始终保持不同步状态，这是因为它们的频率离其它振荡子实现同步以使耦合作用把它们拉入同步核中的频率值太远。

Winfree在作出他的描述时，发现生物学和物理学之间存在一种未曾预料到的联系。他看出相互同步非常类似于相变(如水结成冰以及铁磁体的自发磁化等)。振荡子频率分布的宽度起着温度的作用，而振荡子时间相位的—致则相当于分子取向或电子自旋取向的对齐。

与相变的类比开辟了统计力学的新篇章(统计力学是研究由大量相互作用的亚单元组成的系统的学科)。1975年，京都大学的Yoshiki Kuramoto对Winfree的模型进行了巧妙的改造。Kuramoto的模型的数学构造更简单，因此可以进行非常详细的分析。最近Strogatz和Mirollo以及剑桥大学的Paul C．Matthews一起，发现了Kuramoto的模型和Landau阻尼之间存在一种意外的联系。(Landau阻尼是当电磁波穿过高度稀薄的介质传播时出现的一种令人迷惑不解的等离子体物理学现象。)当我们研究振荡子群体在频率分布太宽而无法实现同步的情况下退化到杂乱状态的过程时，这一联系便出现了。结果表明，同步的消失和电磁波在这类“无碰撞”等离子体中的衰减是由相同的数学机制所支配的。

自从惠更斯注意到摆钟的自发同步以来，耦合振荡子理论已经走过了—段很长的路。同步表面上看来是一类非常自然的行为，但结果证明它既是出人意外又是非常令人感兴趣的。它是一个有待认识的问题，而不是对称性的明显结果。数学家们依靠对称性破缺的理论对相同的、表面上对称的振荡子相互耦合时所出现的一般模式进行了分类。于是，一个以粒子物理学为其最明显起源的数学学科看来支配着瞪羚的跳跃和大象的漫步。与此同时，从统计力学中借鉴的方法则阐明了整个的振荡子群体的行为。看来非常令人感兴趣的是，在激烈变动的等离子体与安静平和的生物振荡子之间存在着一种联系。(等离子体中的原子不断失去其电子，而作为生物振荡子的萤火虫则在河边不声不响地一亮一灭。)但是，存在一条连贯的数学线索把单摆与空间模式、波、混沌和相变等联系起来。这就是数学揭露自然界隐藏着的统—性的威力之所在。